Вимірювання тісноти зв'язку
Вимірювання тісноти зв'язку може бути вирішене за допомогою розрахунку теоретичного кореляційного відношення. Трьома основними цілями аналізу двовимірних даних, представлених парами (х, у), є: (1) опис і розуміння взаємозв'язку, (2) прогнозування та прогноз нового спостереження і (3) коректування та управління процесом. Кореляційний аналіз дозволяє зробити висновок про силу взаємозв'язку, а регресійний аналіз використовується для прогнозування однієї змінної на підставі іншої (як правило, у на підставі х). Двовимірні дані аналізують із використанням діаграми розсіяння в координатах у і х, яка дає візуальне уявлення про взаємозв'язок у даних. Кореляція,або точніше лінійний коефіцієнт кореляції (r), є безрозмірне (що не має одиниць вимірювання) число в діапазоні від -1 до 1, яке характеризує силу взаємозв'язку. Рівність коефіцієнта кореляції 1 свідчить про ідеальний взаємозв'язок у вигляді прямої лінії з нахилом угору. Рівність коефіцієнта кореляції - 1 свідчить про ідеальний взаємозв'язок у вигляді нахиленої вниз (негативно) прямої лінії. Коефіцієнт кореляції говорить про те, наскільки близько до цієї нахиленої прямої лінії розташовані точки діаграми, проте він не характеризує крутизну нахилу цієї лінії. У разі лінійного зв'язку кореляційне відношення може бути замінене лінійним коефіцієнтом кореляції (
де
Коваріація х і у є чисельником у формулі (9.5) для коефіцієнта кореляції. Оскільки одиниці вимірювання коваріації важко інтерпретувати, зручніше працювати з коефіцієнтом кореляції. При аналізі двовимірної діаграми розсіяння можна виявити різні взаємозв'язки. Простою, із погляду аналізу, є лінійний взаємозв'язок,який виражається в тому, що крапки на діаграмі розсіяння з постійним розкидом групуються випадковим чином уздовж прямої лінії. Діаграма свідчить про відсутність взаємозв'язку, якщо крапки розміщені випадково та при переміщенні зліва направо неможливо виявити який-небудь ухил (ні вгору, ні вниз). Двовимірна діаграма розсіяння характеризується нелінійним взаємозв'язком, якщо крапки на ній групуються уподовж кривою, а непрямій лінії. Оскільки кількість видів кривих практично безмежна, аналіз нелінійного взаємозв'язку виявляється набагато складнішим, проте взаємозв'язок можна наблизити до лінійної, застосувавши до даних відповідне перетворення. Проблема нерівної варіації виникає тоді, коли при переміщенні по горизонталі на діаграмі розсіяння варіація крапок по вертикалі сильно змінюється. Нерівна варіація призводить до зниження надійності коефіцієнта кореляції й регресійного аналізу. Проблему нерівної варіації можна вирішити за допомогою відповідних перетворень даних або за допомогою, так званої зваженої регресії. Проблема кластерінга (розділення сукупності на групи однорідних об'єктів) виникає в разі утворення на діаграмі розсіяння окремих, яскраво виражених груп крапок. У таких випадках кожну групу слід аналізувати окремо. Деяка точка даних є викидом (значенням, що різко відхиляється), якщо вона не відповідає взаємозв'язку між рештою даних; значення, що різко відхиляються, можуть спотворити статистичні характеристики двовимірної сукупності даних. Кореляцію не можна розглядати як причинну обумовленість. Коефіцієнт кореляції характеризує зв'язок між числами, але не пояснює її. Кореляція може бути викликана тим, що змінна х впливає на у, або тим, що змінна у впливає на х. Крім того, кореляція може бути викликана також тим, що на х і у впливає якийсь прихований "третій чинник", що створює враження зв'язку між х і у. Терміном помилкова кореляція позначають високу кореляцію, яка виникає завдяки дії деякого третього чинника.
|

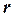 ), вирахуваним за допомогою формул, які тотожні між собою:
), вирахуваним за допомогою формул, які тотожні між собою: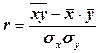 (10.3)
(10.3)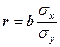 (10.4)
(10.4)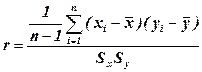 (10.5)
(10.5)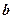 – коефіцієнт регресії в рівнянні зв'язку;
– коефіцієнт регресії в рівнянні зв'язку;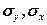 – відповідно середнє квадратичне відхилення в ряду
– відповідно середнє квадратичне відхилення в ряду 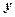 і
і 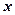 ;
;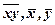 – середні відповідних величин;
– середні відповідних величин;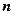 – кількість спостережень;
– кількість спостережень;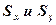 – стандартні відхилення.
– стандартні відхилення.
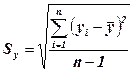 (10.6)
(10.6)


