Задания. Я думаю, они должны состоять из трех частей:Я думаю, они должны состоять из трех частей: 1) Настройка интерферометра (включая знакомство с элементами настройки - аттенюатором, фазовращателем, детекторной головкой – и записью сигнала на осциллографе для последующего переноса на флешку). 2) Знакомство с устройством плазменного резонатора (включая представление о генераторе ВЧ, чтобы не путали его с СВЧ), 3) Снятие характеристик разряда – не менее 5 (?) раз для последующего осреднения данных, поскольку характеристики разряда повторяются не так уж хорошо. Содержательно задача лаб.раб. должна звучать примерно так: исследовать временные характеристики плазменного разряда и определить время его релаксации. Это содержит оценку максимальной концентрации электронов в разряде (по числу полных периодов набега фазы), оценку времени релаксации (по последнему участку спада концентрации).
Рассмотрим условия интерференции (рис. 4, а). Мы настроили интерферометр без плазмы таким образом, что детектор показывает нулевой сигнал (Uд = 0). Это означает, что сигналы обоих плеч равны по величине и совпадают по фазе. (Обратим внимание на то, что в интерферометре использован разностный детектор, выдающий на выходе сигнал, равный разности сигналов обоих плеч. При их равенстве и совпадении по фазе на выходе детектора будет нулевое напряжение).
Когда концентрация плазмы была велика, сигнал по плечу 2 не проходил и детектор выдавал на выходе сигнал, соответствующий только величине сигнала в плече 1 (напряжение U2 на рис. 4,а). Пусть в момент t0 мы выключили ВЧ генератор, и концентрация зарядов плазмы начала экспоненциально уменьшаться. До момента t1 она оставалась такой, что выполнялось условие fp > fСВЧ и излучение не проходило через плазму. Начиная с t1, излучение начало проходить через плазму. Если бы оно проходило без сдвига фазы и без затухания (без потерь), то выходное напряжение детектора сразу уменьшилось бы до нуля, поскольку именно так был настроен наш интерферометр. Действие плазмы на прохождение СВЧ сигнала. В принципе плазма может внести в сигнал как затухание (уменьшение амплитуды проходящего сигнала), так и сдвиг фазы. Однако, в наших условиях длина пробега молекул газа в колбе больше длины самой колбы. В этих условиях столкновением заряженных частиц с нейтральными атомами можно пренебречь. А это значит, что потери энергии СВЧ поля будут пренебрежимо малы и сигнал проходит через плазму без заметного уменьшения амплитуды. Если бы сдвига фаз волн в обоих плечах не было, то сигнал детектора упал бы до нуля. Теперь о сдвиге фазы. Плазма в пренебрежении соударениями имеет показатель преломления μ; [2,3]
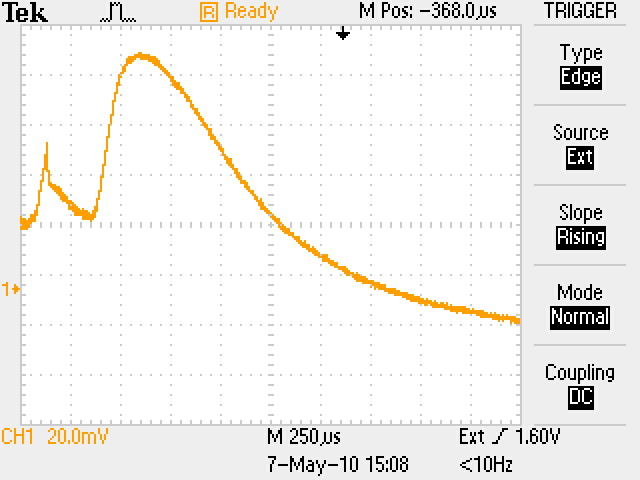
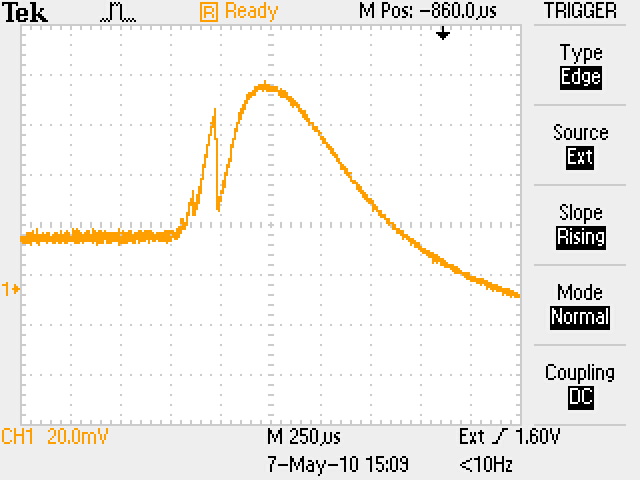
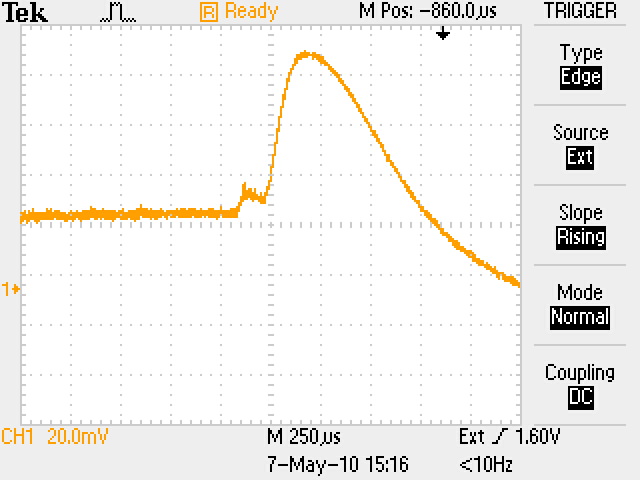
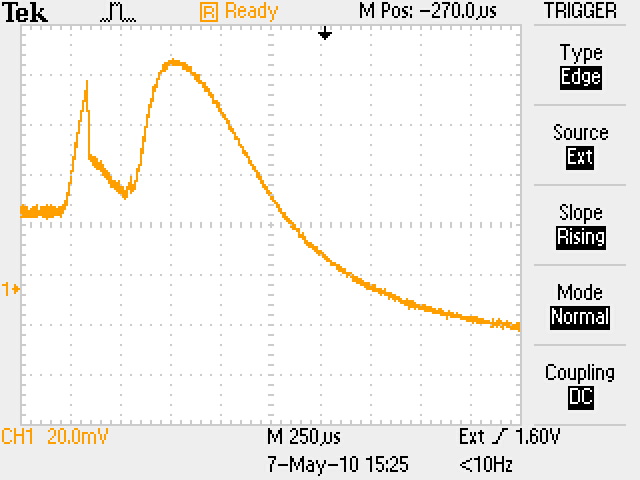
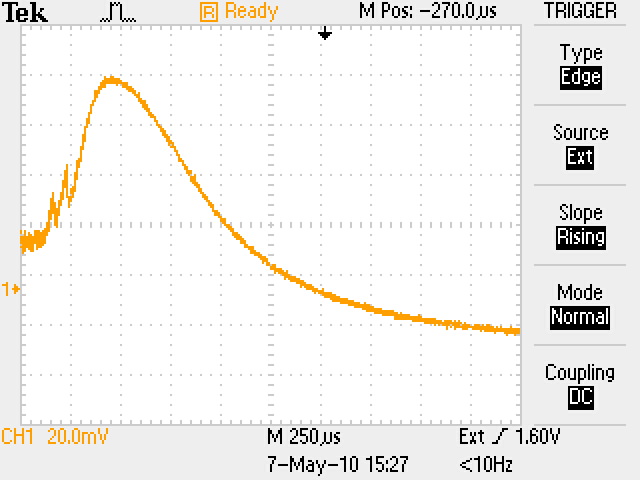
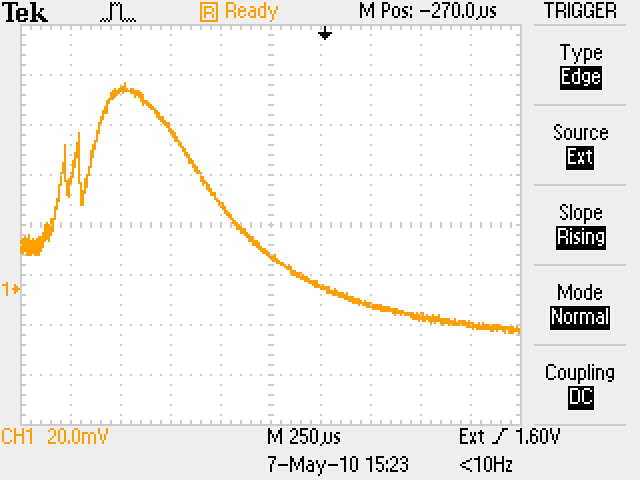
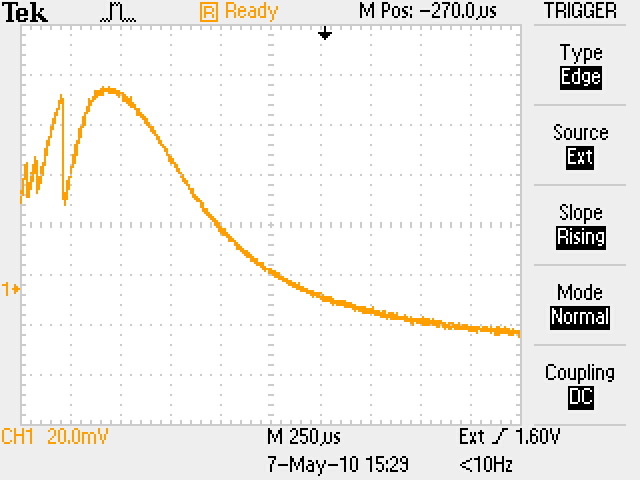
Здесь nкр = 1,24∙ 10-8f2СВЧ см-3 – критическая концентрация плазмы в момент времени t1, начиная с которой излучение будет проходить через нее, n(t) – уменьшающаяся концентрация электронов плазмы, начиная с момента времени t1. В момент времени t1 плазменная частота равна частоте СВЧ сигнала fp = fСВЧ, а далее плазменная частота становится меньше частоты СВЧ сигнала в соответствии с уменьшением концентрации (3). Таким образом, показатель преломления плазмы изменяется от 0 (на самом деле примерно от 0,1 из-за соударений) до 1 по мере уменьшения концентрации электронов. Когда он станет таким, что сдвиг фазы на длине колбы будет равен π, сигнал в плече 2 станет противофазным относительно сигнала плеча 1 и равным по амплитуде. Детектор выдаст максимальный сигнал (U = U1+U2 на рис. 4, а). Если затухание сигнала в плазме равно нулю, то U1=U2, что мы и наблюдаем на осциллограммах. Это свидетельствует о справедливости нашего предположения, что соударениями в нашем случае можно пренебречь, по крайней мере в случае nе ≥ n(t), соответствующей времени, близкому к t2 и далее. Рассмотрим полученные осциллограммы. Представим кривые обобщенным графиком, показанным на рис. 4,б. Под каждой осциллограммой я указал времена t1 и t2, соответствующие обозначениям рис. 4,б.
t1 = 550 t2 =1100 t1 + t2 = 1650 t1 = 400 t2 = 750 t1 + t2 =1150
t1 = 550 t2 = 700 t1 + t2 = 1250 t1 =300 t2 =650 t1 + t2 =950
t1 =450 t2 =450 t1 + t2 = 900 t1 = 300 t2 = 600 t1 + t2 = 900
t1 =300 t2 =600 t1 + t2 =900 t1 =550 t2 =550 t1 + t2 =1100
t1 = 450 t2 =600 t1 + t2 = 1050 t1 =400 t2 = 600 t1 + t2 =1000
t1 = 400 t2 =750 t1 + t2 = 1150 t1 =300 t2 = 600 t1 + t2 =900
Усредним времена по всем осциллограммам. Получим t1 ≈ 400 мкс, t2 ≈ 650 мкс, t1 + t2 ≈ 1050 мкс. Начиная с максимума кривая ведет себя монотонно, без всяких "выбросов". Причем сам максимум (напряжение U1) равен по величине напряжению U2. Это означает, что в точке максимума волна в плече 2 сдвинута относительно волны в плече 1 ровно на π (волны плеч приходит в детектор в противофазе). Для курсовой работы мы будем анализировать именно этот участок кривой – экспоненциальный участок на временах равных и больше времени достижения максимума. (Участок с "выбросами", я поясню для вас ниже, но это пояснение в тексте курсовой работы можно не помещать). Если бы волны были сдвинуты на величину, кратную π (кратность больше единицы), то мы наблюдали бы более чем 1 максимум на временах больше t1. Рассчитаем сдвиг фаз в соответствии с формулой (21) для показателя преломления плазмы. Геометрическая длина колбы (геометрический путь для волны в вакууме) L0 = 9 см. Оптический путь L = μL0. Поскольку на длине колбы волна получила сдвиг по фазе на π, то это означает, что оптический путь оказался ровно на λ;/2 короче, чем геометрический. (Короче, потому что согласно формуле 21 показатель преломления плазмы меньше 1). Таким образом, L0 – L = λ;/2, откуда (1 – μ;) L0 = λ;/2 μ = 1 – λ/2L0 = 0,82. (22) Из формулы (21), имеем μ2 = 1 – n(t)/nкр. Для момента времени t, соответствующего максимуму кривой, (1 – λ/2L0)2 = 1 – n(t)/nкр = 0.67 (23) Для СВЧ излучения с длиной волны 3,2 см получаем nкр = 1,24∙108f2 = 1,24∙10-8(3/3,2∙1010)2=1,1∙1012 см-3. С учетом этого из (23) получаем концентрацию электронов, соответствующую максимуму кривой nмак: nмак = (1 – 0,67) nкр = 0,36∙1012 см-3. Оценим концентрацию электронов, при котором начинается прохождение СВЧ излучения через плазму. Будем считать, что после начала прохождения излучения концентрация электронов уменьшается по экспоненциальному закону n(t) = n0exp(-t/τ), где τ – постоянная времени падения концентрации. Учитывая, что среднее время расположения максимума равно t1 = 400 мкс, получаем n (при t=400мкс) = nкрexp(-400/τ) = 0,36∙1012 см-3. Отсюда τ; (мкс) = 400/(ln nкр/nмак) = 358 мкс. Это с точностью до 10% совпадает с экспериментально полученным средним временем t1 = 400 мкс.
Мы можем это проверить, сняв точки кривой на последнем экспоненциальном участке (рис. 4, б). Для этого нужно будет обработать те осциллограммы, на которых экспоненциальная часть представлена достаточно хорошо (7 осциллограмм). Каждую кривую представить 6…7 точками: напряжение U(t). Затем в Excel построить кривые и аппроксимировать их экспоненциальными трендами. Вычислить среднюю постоянную времени τср по всем осциллограммам и сравнить ее с вычисленными выше. Для примера я построил одну такую аппроксимацию. Для нее τ = 500 мкс, что на 20% выше расчетных. Теперь обещанное объяснение начальной части кривых (для t1). Здесь показатель преломления растет примерно с 0,1 до 0.82. Для минимального показателя преломления μ = 0,1 это даст разницу геометрического и оптического пути L0 – L = L0 (1– μ;) = 0.9 L0 = 8,1 мм, что составляет 8,1/3,2 = 2,5 длины волны λ = 3,2 см. Это означает, что на отрезке времени t1 (до нашего максимума) кривая еще дважды должна была достигать максимумов и минимумов. Это мы и видим на целом ряде осциллограмм. Однако из-за экспоненциальной зависимости спада концентрации эти максимумы и минимумы чередуются весьма быстро во времени. Возможно, такие малые времена (такие быстрые процессы) не успевают "отрабатывать" СВЧ диоды. Поэтому мы видим только "выбросы" вместо полноценных максимумов и минимумов.
Литература 1. Диагностика плазмы. Под ред.Р. Хаддлстоуна и С. Леонарда. Пер. с англ. – М.: Мир, 1967. – 516 с. 2. Диагностика плазмы. Сборник статей. Под ред.акад. Б.П. Константинова. – М.: Госатомиздат, 1963. – 302 с. 3. Подгорный И.М. Лекции по диагностике плазмы. – М.: Атомиздат, 1968. 220 с. 4. М. Хилд, С. Уортон. Микроволновая диагностика плазмы. /Пер. с англ. под ред. И.С. Шпигеля. – М.: Атомиздат, 1968. – 392 с. 5. Хиппель А.Р. Диэлектрики и волны. Пер. с англ. – М.: ИЛ, 1960. – 438 с.
|

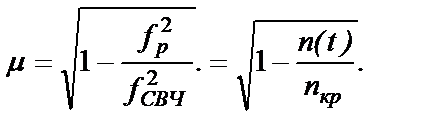 (21)
(21)





 Будет ли сохраняться эта постоянная времени уменьшения концентрации электронов плазмы на последнем участке кривой (при t > t1)?
Будет ли сохраняться эта постоянная времени уменьшения концентрации электронов плазмы на последнем участке кривой (при t > t1)?


