Вклад Леонардо да Винчи в теоретическую механику
Вернер Содэл, Вернард Фоли Vernard Foley, Werner Soedel. Leonardo’s Contributions to Theoretical Mechanics Тщательное изучение рисунков Леонардо да Винчи, в частности тех, на которых изображен арбалет, показывает, что его идеи имели отношение к эволюции четырех представлений в механике
Н ЕКОТОРЫЕ историки, исследования которых относятся к эпохе Возрождения, высказывали мнение, что, хотя Леонардо да Винчи был талантливым во многих областях, он тем не менее не внес значительного вклада в такую точную науку, как теоретическая механика. Однако тщательный анализ его недавно обнаруженных рукописей и в особенности имеющихся в них рисунков убеждает в обратном. Работы Леонардо да Винчи по изучению действия различных видов оружия, в частности арбалета, по-видимому, были одной из причин его интереса к механике. Предметами его интереса в этой области, говоря современным языком, были законы сложения скоростей и сложения сил, понятие нейтральной плоскости и положение центра тяжести при движении тела. Спор о том, какой вклад внес Леонардо да Винчи в точные науки, частично связан с историей его записных книжек. После его смерти они попали в руки частных коллекционеров и в течение длительного времени доступ к ним был ограничен. Публиковать эти записные книжки начали лишь в конце XIX в. и вскоре стали считать, что Леонардо да Винчи на столетия опередил многие открытия. Однако восхищение именем Леонардо да Винчи вызывало интерес и к трудам его предшественников и современников. Было установлено, что Леонардо да Винчи многое перенял из этих источников и иногда даже копировал имеющиеся в них рисунки. Поэтому стало распространяться мнение, что он вообще не создал что-либо оригинальное, заслуживающее внимания. Две новые рукописи Леонардо да Винчи, обнаруженные около 20 лет назад в Мадриде и известные под названием "Мадридские рукописи", показывают, что это мнение необоснованно. Л. Рети из Калифорнийского университета в Лос-Анджелесе, первым изучавший рукописи (в этой работе ему большую помощь оказал Б. Дибнер), отмечал, что они должны сыграть важную роль в "восстановлении репутации" Леонардо да Винчи как исследователя природы. Следует иметь в виду, что Леонардо да Винчи обучался в мастерских живописцев и скульпторов, поэтому его основными "инструментами" в познании мира были глаза и руки. Мы считаем, что вклад Леонардо да Винчи в теоретическую механику может быть оценен в большей степени путем более внимательного изучения его рисунков, а не текстов рукописей и имеющихся в них математических выкладок.
Н АЧНЕМ с примера, отражающего настойчивые попытки Леонардо да Винчи решить задачи, связанные с усовершенствованием конструкции оружия (никогда полностью не решенные), вызвавшие у него интерес к законам сложения скоростей и сложения сил. Несмотря на быстрое развитие порохового оружия в период жизни Леонардо да Винчи, лук, арбалет и копье еще продолжали оставаться распространенными видами оружия. Особенно много внимания Леонардо да Винчи уделял такому старинному оружию, как арбалет. Часто бывает, что конструкция той или иной системы достигает совершенства только после того, как ею заинтересуются потомки, причем процесс совершенствования этой системы может приводить к фундаментальным научным результатам. Плодотворные экспериментальные работы по совершенствованию арбалетов проводились и раньше, до Леонардо да Винчи. Например, в арбалете стали использовать укороченные стрелы, которые имели примерно в 2 раза лучшие аэродинамические характеристики, чем обычные лучные стрелы. Кроме того, было положено начало изучению основных принципов, лежащих в основе стрельбы из арбалета, о чем свидетельствует рисунок неизвестного художника, который обнаружен в рукописи, известной под названием "Гуситские войны". Этот рисунок отражает попытку представить арбалет на основе понятия круга: станок, или ложа, арбалета образует диаметр круга, его спусковой механизм находится в центре круга, дуга арбалета составляет треть дуги окружности, а тетива в ненатянутом положении делит радиус пополам. В определенном смысле этот рисунок отражает раннюю стадию инженерной теории, когда предпринимались попытки подчинить конструкцию устройства идеальной геометрической форме. Иногда такой подход оказывался плодотворным. В отношении арбалета целесообразность этого подхода состояла хотя бы в том, что дуга, имеющая постоянную кривизну, служит дольше. Если этого достичь невозможно, то изменение радиуса дуги должно быть как можно более плавным. Стремясь не ограничиваться традиционными конструктивными решениями, Леонардо да Винчи обдумывал такую конструкцию арбалета, которая позволяла бы стрелять только наконечником стрелы, оставляя ее древко неподвижным. По-видимому, он понимал, что за счет уменьшения массы снаряда можно увеличить его начальную скорость. В некоторых из своих конструкций арбалетов он предлагал использовать несколько дуг, действующих либо одновременно, либо последовательно. В последнем случае самая большая и массивная дуга приводила бы в действие меньшую по размерам и более легкую дугу, а та и свою очередь еще меньшую и т.д. Выстрел стрелой производился бы на последней дуге. Очевидно, что Леонардо да Винчи рассматривал этот процесс с точки зрения сложения скоростей. Например, он отмечает, что дальность стрельбы из арбалета будет максимальной, если произвести выстрел на скаку с лошади, мчащейся галопом, и в момент выстрела податься вперед. В действительности это не привело бы к значительному увеличению скорости стрелы. Тем не менее идеи Леонардо да Винчи имели прямое отношение к разгоравшемуся спору относительно того, возможно ли бесконечное увеличение скорости. Позже ученые начали склоняться к выводу, что этот процесс не имеет предела. Такая точка зрения существовала до тех пор, пока Эйнштейн не выдвинул свой постулат, из которого следовало, что ни одно тело не может двигаться со скоростью, превышающей скорость света. Однако при скоростях, много меньших скорости света, закон сложения скоростей (на основе принципа относительности Галилея. – Ред.) остается справедливым.
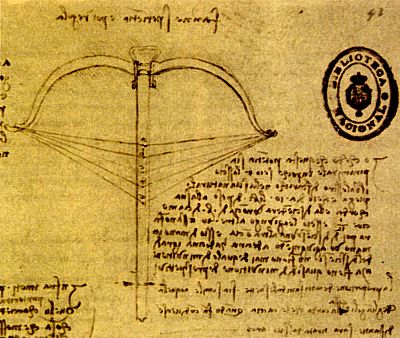
З АКОН сложения сил, или параллелограмм сил, был открыт уже после Леонардо да Винчи. Этот закон рассматривается в том разделе механики, который позволяет ответить на вопрос, что происходит, когда две или более сил взаимодействуют под различными углами. Сегодня эта задача решается просто: чертят параллелограмм (или параллелограммы) сил и находят результирующую силу, направленную по диагонали. Возможно, что Леонардо да Винчи занимался, хотя и неосознанно, решением такой задачи, когда он анализировал действие арбалета, стремясь найти то или иное конструктивное решение. Силы, направленные под углом друг к другу, возникают, например, при натяжении тетивы. При изготовлении арбалета важно добиться симметричности усилий, возникающих в каждом крыле. В противном случае стрела может сместиться при выстреле в сторону из своей канавки, и точность стрельбы тем самым будет нарушена. Обычно арбалетчики, подготавливая свое оружие к стрельбе, проверяли, одинаков ли изгиб крыльев его дуги. Сегодня таким образом проверяются все луки и арбалеты. Оружие подвешивается на стене так, чтобы его тетива была горизонтальна, а дуга выпуклой частью обращена вверх. К середине тетивы подвешиваются различные грузы. Каждый груз вызывает определенный изгиб дуги, что позволяет проверить симметричность действия крыльев. Легче всего это сделать, наблюдая, опускается ли при увеличении груза центр тетивы по вертикали или отходит от нее. Этот способ, возможно, навел Леонардо да Винчи на мысль использовать диаграммы (обнаружены в "Мадридских рукописях"), в которых смешение концов дуги (с учетом положения центра тетивы) представлено в зависимости от величины подвешенного груза. Он понимал, что сила, необходимая для того, чтобы дуга начала сгибаться, поначалу невелика и возрастает с увеличением смешения концов дуги. (В основе этого явления лежит закон, сформулированный гораздо позже Робертом Гуком: абсолютная величина смешения в результате деформации тела пропорциональна приложенной силе.) Зависимость между смещением концов дуги арбалета и величиной подвешенного к тетиве груза Леонардо да Винчи называл "пирамидальной", поскольку, как в пирамиде противоположные грани расходятся по мере удаления от точки пересечения, так и эта зависимость становится все более заметной по мере смещения концов дуги. Отмечая изменение положения тетивы в зависимости от величины груза, он, однако, заметил нелинейности. Одна из них состояла в том, что, хотя смещение концов дуги линейно зависело от величины груза, между смешением тетивы и величиной груза линейная зависимость отсутствовала. На основании этого наблюдения Леонардо да Винчи, по-видимому, пытался найти объяснение тому факту, что в некоторых арбалетах тетива, отпущенная после приложения к ней силы определенной величины, движется сначала быстрее, чем в момент приближения к своему исходному положению. Такая нелинейность, возможно, и наблюдалась при пользовании арбалетами с плохо изготовленными дугами. Вероятно, что выводы Леонардо да Винчи основаны на ошибочном рассуждении, а не на расчетах, хотя иногда он все же прибегал к вычислениям. Тем не менее эта задача вызвала у него глубокий интерес к анализу конструкции арбалета. Действительно ли стрела, быстро набравшая скорость в начале выстрела, начинает двигаться быстрее тетивы и оторвется от нее до того, как тетива возвратится в исходное положение? Не имея четкого представления о таких понятиях, как инерция, сила и ускорение, Леонардо да Винчи, естественно, не мог найти окончательного ответа на этот вопрос. На страницах его рукописи встречаются рассуждения противоположного характера: в некоторых из них он склонен ответить на этот вопрос положительно, в других – отрицательно. Интерес Леонардо да Винчи к этой проблеме привел его к дальнейшим попыткам усовершенствовать конструкцию арбалета. Это говорит о том, что интуитивно он догадывался о существовании закона, впоследствии получившего название "закон сложения сил".
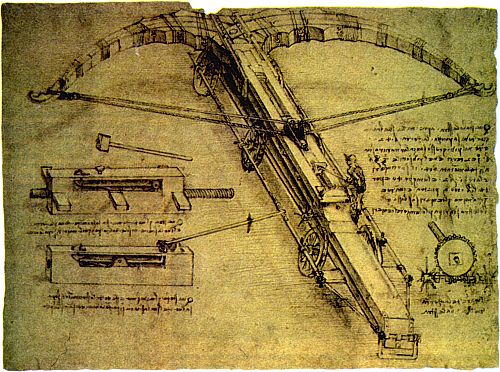
Л ЕОНАРДО да Винчи не ограничился только проблемой скорости движения стрелы и действия сил натяжения в арбалете. Например, его интересовало также, увеличится ли дальность полета стрелы в два раза, если в два раза увеличить вес дуги арбалета. Если измерить суммарный вес всех стрел, расположенных одна за другой впритык и составляющих непрерывную линию, длина которой равна максимальной дальности полета, то будет ли этот вес равен силе, с которой тетива действует на стрелу? Иногда Леонардо да Винчи действительно смотрел глубоко, например в поисках ответа на вопрос, свидетельствует ли вибрация тетивы сразу после выстрела о потере энергии дугой? В итоге в "Мадридской рукописи" I, касаясь соотношения между усилием на дуге и смещением тетивы, Леонардо да Винчи утверждает: "Сила, вынуждающая тетиву арбалета двигаться, увеличивается по мере уменьшения угла в центре тетивы". Тот факт, что это утверждение больше не встречается нигде в его записях, может означать, что такой вывод был сделан им окончательно. Несомненно, он применял его в многократных попытках усовершенствовать конструкцию арбалета с так называемыми блочными дугами. Блочные дуги, в которых тетива пропущена через блоки, известны современным стрелкам из лука. Эти дуги позволяют достичь высокой скорости полета стрелы. Законы, лежащие в основе их действия, сейчас хорошо известны. Леонардо да Винчи не имел столь же полного представления о действии блочных дуг, однако он изобрел арбалеты, в которых тетива пропускалась через блоки. В его арбалетах блоки обычно имели жесткое крепление: они не перемещались вместе с концами дуги, как в современных арбалетах и луках. Поэтому дуга в конструкции арбалета Леонардо да Винчи не оказывала такого же действия, как в современных блочных дугах. Так или иначе, Леонардо да Винчи, очевидно, намеревался изготовить дугу, конструкция которой позволяла бы решить проблему "тетива – угол", т.е. увеличение силы, действующей на стрелу, достигалось бы за счет уменьшения угла в центре тетивы. Кроме того, он пытался уменьшить потери энергии при стрельбе из арбалета. В основной конструкции арбалета Леонардо да Винчи очень гибкая дуга укреплялась на станине. На некоторых рисунках видно, что при максимальном натяжении тетивы дуга изгибалась почти в окружность. От концов дуги тетива с каждой стороны пропускалась через пару блоков, укрепленных впереди станины рядом с направляющей канавкой для стрелы, а затем шла к спусковому устройству. Леонардо да Винчи, по-видимому, нигде не дал объяснения своей конструкции, однако ее схема неоднократно встречается в его рисунках вместе с изображением арбалета (также с сильно изогнутой дугой), в котором натянутая тетива, идущая от концов дуги к спусковому устройству, имеет V-образную форму. Представляется наиболее вероятным, что Леонардо да Винчи стремился максимально уменьшить угол в центре тетивы с тем, чтобы стрела при выстреле получала большее ускорение. Возможно, что и блоки он использовал для того, чтобы угол между тетивой и крыльями арбалета оставался как можно дольше близким к 90°. Интуитивное представление о законе сложения сил помогло ему радикально изменить проверенную временем конструкцию арбалета на основе количественного соотношения между энергией, "запасенной" в дуге арбалета, и скоростью движения стрелы. Несомненно, он имел представление о механической эффективности своей конструкции и пытался дополнительно усовершенствовать ее. Блочная дуга Леонардо да Винчи, видимо, была непрактичной, поскольку резкое натяжение тетивы приводило к значительному ее изгибу. Такую значительную деформацию могли выдержать лишь составные дуги, изготовленные особым образом.
С ОСТАВНЫЕ дуги использовались при жизни Леонардо да Винчи и, возможно, именно они вызвали у него интерес к той проблеме, попытки решить которую привели его к представлению о том, что именуется нейтральной плоскостью. Исследование этой проблемы было связано и с более глубоким изучением поведения материалов под действием механического напряжения. В типичной составной дуге, применявшейся в эпоху Леонардо да Винчи, внешняя и внутренняя стороны крыльев арбалета изготавливались из различных материалов. Внутренняя сторона, испытывавшая сжатие, обычно изготавливалась из рога, а внешняя, работавшая на растяжение, – из сухожилий. Каждый из этих материалов прочнее дерева. Между внешней и внутренней сторонами дуги использовался деревянный слой, достаточно прочный, чтобы придать крыльям жесткость. Крылья такой дуги можно было сгибать более чем на 180°. Леонардо да Винчи имел некоторое представление о том, как изготавливали такую дугу, а проблема выбора материалов, которые могли бы выдерживать сильное натяжение и сжатие, возможно, привела его к глубокому пониманию того, как возникают напряжения в той или иной конструкции. На двух небольших рисунках (обнаруженных в "Мадридской рукописи" I) он изобразил плоскую пружину в двух состояниях – деформированном и недеформированном. В центре деформированной пружины он начертил две параллельные линии, симметричные относительно центральной точки. При сгибании пружины эти линии расходятся с выпуклой стороны и сходятся – с вогнутой. Эти рисунки сопровождает подпись, в которой Леонардо да Винчи отмечает, что при сгибании пружины выпуклая часть становится толще, а вогнутая – тоньше. "Такая модификация является пирамидальной и, следовательно, никогда не будет изменяться в центре пружины". Иными словами, расстояние между первоначально параллельными линиями будет возрастать в верхней части по мере его уменьшения в нижней. Центральная часть пружины служит своего рода балансом между двумя сторонами и представляет собой зону, где напряжение равно нулю, т.е. нейтральную плоскость. Леонардо да Винчи понимал также, что как натяжение, так и сжатие увеличиваются пропорционально расстоянию до нейтральной зоны. Если определить точки, где напряжения равны нулю, т.е. найти таким образом нейтральную плоскость, то можно проанализировать, как происходит возрастание нагрузок; нейтральная плоскость при этом будет служить плоскостью отсчета. Не прибегая к связанным между собой понятиям нейтральной плоскости и пропорционального возрастания напряжений, трудно, а зачастую просто невозможно (особенно без помощи компьютера) правильно предсказать, как будут увеличиваться нагрузки, и проектировать надежный элемент конструкции, например, балку. Компьютер может разбить детали конструкции или машины на части и оценить напряжения в каждой из них, но даже и в этом случае обычно используется понятие нейтральной плоскости, поскольку это облегчает программирование. Итак, упомянутые выше два рисунка показывают, что Леонардо да Винчи имел дело с одним из основных понятий механики. (К. Замматио, изучающий наследие Леонардо да Винчи, также отмечает, что эти рисунки имеют большое значение.) Из рисунков Леонардо да Винчи видно, что представление о нейтральной плоскости возникло у него и при изучении действия арбалета. Примером является его рисунок гигантской катапульты для стрельбы камнями. Сгибание дуги этого оружия производилось с помощью винтового ворота; камень вылетал из кармана, расположенного в центре сдвоенной тетивы. Как ворот, так и карман для камня нарисованы (в увеличенном масштабе) такими же, как и на рисунках арбалета. Однако Леонардо да Винчи, по-видимому, понимал, что увеличение размера дуги приведет к сложным проблемам. Судя по рисункам Леонардо да Винчи, на которых изображена нейтральная зона, ему было известно, что (для данного угла сгибания) напряжения в дуге увеличиваются пропорционально ее толщине. Чтобы напряжения не достигали критической величины, он изменил конструкцию гигантской дуги. Передняя (фронтальная) ее часть, испытывавшая растяжение, по его представлениям, должна изготавливаться из цельного бревна, а задняя ее часть (тыльная), работающая на сжатие, – из отдельных блоков, закрепленных позади передней части. Форма этих блоков была такова, что они могли соприкасаться друг с другом только при максимальном изгибе дуги. Эта конструкция, так же как и другие, показывает, что Леонардо да Винчи считал, что силы растяжения и сжатия следует рассматривать отдельно друг от друга.
П ОСЛЕДНИЙ пример, который мы рассмотрим, также служит подтверждением тому, что серьезный анализ даже простых проблем механики показывает, что в их основе лежат фундаментальные законы. Этот пример связан с вопросом о положении центра тяжести тела. Другой небольшой, но очень важный рисунок (также обнаруженный в "Мадридской рукописи" I) позволяет установить связь между размышлениями Леонардо да Винчи относительно действия арбалета и его более поздними работами по теории полета. На этом рисунке изображен арбалет, выстрел из которого производится вертикально вверх. В начале полета стрела направлена острием вниз (Леонардо да Винчи, возможно, видел, как иногда шутки ради арбалетчики заряжали так свое оружие). По мере движения вверх стрела разворачивается острием вперед. При движении вниз процесс повторяется в обратном порядке. Леонардо да Винчи отмечает, что при движении как вверх, так и вниз стрела имеет одинаковую траекторию. "Центр естественного движения (под действием силы тяжести) и центр насильственного движения (вызванного другими силами) один и тот же… Центр тяжести стрелы находится в одной и той же ее точке на протяжении всего ее движения, будь оно насильственным или естественным". Таким образом, на рисунке стрела изображена вращающейся вокруг своего центра тяжести, который движется вдоль траектории полета. Иными словами, Леонардо да Винчи начинал понимать, что движение стрелы можно рассматривать как движение ее центра тяжести с определенной скоростью вдоль данной траектории. Поэтому его рисунок имеет значение и для истории развития теории вращения твердого тела, поскольку такой подход позволял упростить задачу настолько, что движение тела можно было анализировать математически. Более важным, однако, является то, что рисунок, на наш взгляд, представляет собой первую попытку применить понятие центра тяжести в динамике. (Архимед пользовался этим понятием в статике.) М. Кладжет из Института высших исследований в Принстоне, известный своими работами по истории механики в средние века, разделяет эту точку зрения. Один рисунок Леонардо да Винчи, где изображен центр тяжести движущегося тела, был известен еще до открытия "Мадридских рукописей". На этом рисунке, обнаруженном в записной книжке, известной под названием "Кодекс Форстера" II, изображен падающий и переворачивающийся кубик. В подписи к этому рисунку отмечается, что центр тяжести кубика все время остается на траектории, по которой он движется вниз. Рисунок стрелы арбалета, обнаруженный в "Мадридской рукописи", очевидно, был сделан раньше этих двух рисунков, и его можно рассматривать как исходную точку исследований Леонардо да Винчи в области теории полета. В рукописи "Sul Volo" и других своих записях Леонардо да Винчи отмечает, что устойчивость полета птицы достигается только тогда, когда ее центр тяжести находится впереди центра сопротивления (точки, в которой давление спереди и сзади одинаково). Этот функциональный принцип, использовавшийся Леонардо да Винчи в теории полета птиц, и сейчас имеет важное значение в теории полета самолетов и ракет. Справедливость заключения Леонардо да Винчи относительно условия устойчивости полета несложно проверить экспериментально. Мы выбрали слабую дугу и тяжелую стрелу (чтобы ее скорость была относительно низкой) и то место древка стрелы, где находился центр тяжести, обернули яркой оранжевой лентой. К переднему концу стрелы была приделана тяжелая насадка с выемкой для тетивы, что облегчало наблюдения за стрелой. Полет стрелы наблюдался на темном фоне, например на фоне деревьев. Несмотря на то что стрелки мы неважные, нам удалось установить, что положение центра тяжести всегда имело важное значение; во многих случаях стрела переворачивалась вокруг своего центра тяжести, оранжевая метка при этом продолжала перемещаться вдоль неизменной траектории.
|