Электромеханические свойства двигателей
Уравнение электрического равновесия цепи якоря двигателя постоянного тока (ДПТ) записывают следующим образом: U = Е+ IR = КФω + I(Rя+ Rд), где U – напряжение, приложенное к цепи ДПТ, В; Е – ЭДС, наведенная в обмотке якоря ДПТ, В; I – ток в цепи якоря ДПТ, А; R – общее сопротивление цепи якоря, Ом; К – безразмерный коэффициент, определяемый конструктивными параметрами двигателя; Ф – магнитный поток ДПТ, Вб; ω – угловая скорость вращения якоря ДПТ (в дальнейшем просто скорость), рад/с; Rя – внутреннее сопротивление цепи якоря ДПТ, состоящее из сопротивлений последовательно соединенных обмоток якоря rо.я, дополнительных полюсов rд.п и компенсационной rк.ощеточного контакта rщ, а также сопротивления последовательной обмотки возбуждения rо.в (для ДПТ последовательного возбуждения); Rд – сопротивление добавочного резистора, включаемого последовательно в цепь якоря, Ом. Внутреннее сопротивление цепи якоря ДПТ с независимым возбуждением (НВ) и ДПТ последовательного возбуждения (ПВ) рассчитывается соответственно по формулам: Rя ≈ 0,5(1 – ηн)Uн/Iн = 0,5(1 – ηн)Rн, Rя ≈ 0,75(1 – ηн)Rн, где ηн, Uн, Iн, Rн – соответственно номинальные КПД, напряжение, В, ток, А, и сопротивление, Ом. Электродвижущая сила (ЭДС), наведенная в обмотке ДПТ при номинальной скорости ωн и номинальном магнитном потоке Фн, Ен = Снωн = Uн – IнRя = Uн – ΔUя, где Сн – коэффициент пропорциональности между ЭДС и скоростью, а также между электромагнитным моментом и током якоря в ДПТ при неизменном магнитном потоке возбуждения Фн. Номинальный электромагнитный вращающий момент ДПТ Мэ.н = КФнIн = Мн + Мх.х, где М н – номинальный вращающий момент на валу электродвигателя, Н·м; Мх.х – момент холостого хода (момент потерь) двигателя, Н·м. Этот момент мал относительно момента на валу двигателя, поэтому в приближенных расчетах им можно пренебречь и считать, что момент на валу двигателя равен его электромагнитному моменту. Уравнение злектромеханической характеристики ДПТ НВ записывают следующим образом: ω = (U – IR)/С = ω – Δω, где ω0 – скорость якоря при идеальном холостом ходе ДПТ, рад/с; Δω – статическое падение скорости якоря, рад/с. Уравнение механической характеристики ДПТ НВ записывают так: ω = U/С – МR/С2 = ω0 – Δω, где М – вращающий момент на валу двигателя, Н·м. Мощность, потребляемая двигателем из электрической сети при номинальной нагрузке, Рэ.н = UнIн = Рн/ηн = Мнωн/ηн, где Рн – номинальная механическая мощность на валу двигателя, Вт; Номинальный вращающий момент на валу двигателя Мн = Рн · 103/ωн = Рн · 103/(0,15пн). Скорость идеального холостого хода
Сопротивления добавочных резисторов, включаемых в цепь якоря ДПТ для ограничения тока при пуске, рекуперативном и динамическом торможении, а также при торможении противовключением рассчитывают по формулам: Rд.п.т = Uс/Iп – Rя; Rд.р.т = (Ея - Uс)/Iт – Rя; Rд.д.т = Ея/Iт – Rя; Rд.т.п = (Uс + Ея) /Iт – Rя, где Iп и Iт – допустимые (предельные) начальные значения тока при пуске и торможении; U с,Ея – напряжение сети и ЭДС якоря. Физические величины, выраженные в относительных единицах: вращающий момент М* = М/Мн; магнитный поток Ф* = Ф/Фн; напряжение U* = U/Uн; перепад скорости δ = (ω0 – ω)/ω0 = Δω/ω0; скорость якоря ДПТ НВ ω* = ω/ω0; скорость якоря ДПТ ПВ ω* = ω/ωн; сопротивление R* = R/Rн при I = Iн, R = δ; ток I* = I/Iн при Ф = Фн. Полные потери мощности в двигателе при Р = Р н
Активное сопротивление фазы обмотки ротора асинхронного двигателя (АД) с фазным ротором R*2 = R2/R2н = R2нsн/R2н = sн; скольжение АД s = (ω0 – ω)/ω0 = 1 – ω*; номинальное сопротивление фазы ротора АД с фазным ротором
угловая скорость вращения магнитного поля статора АД ω0 = ω1 = 2 πf 1/ p = π n 1/30 ≈ 0,105 п 1, где f 1 – частота питающего напряжения, Гц; р – число пар полюсов; п 1 – частота вращения магнитного поля статора, мин-1, частота (синхронная) вращения магнитного поля статора АД п 1 = 60 f 1/ р; скорость вращения ротора АД ω = ω0(1 – s); потери мощности в цепи ротора АД ΔP2 = Рэ – Рмх = Мω0 – Мω = Мω0s = 3(I´2)2R´2 = 3(I´2)R2, где Р мх – механическая мощность на валу ротора, Вт; I’´2 и R´2 – соответственно ток и активное сопротивление, приведенные к обмотке статора. Уравнение механической характеристики АД записывают следующим образом:
где М к – критический (максимальный) момент двигателя, Н·м; а = R1 /R´2 – отношение активного сопротивления R1 фазы обмотки статора АД к приведенному активному сопротивлению R´2фазы обмотки ротора; sк – критическое скольжение, соответствующее критическому моменту. Критическое скольжение АД при а = 1
Критическое скольжение при а ≡ 0
Частота тока ротора f2 = f1s. Общее активное сопротивление одной фазы ротора АД с фазным ротором Rр = R2 + R2д.р, где R2д.р – сопротивление добавочного резистора, включаемого в цепь ротора, Ом. Угловая скорость вращения якоря ДПТ ПВ на реостатной характеристике при фиксированном значении тока Ii.
где ωеi – угловая скорость на естественной электромеханической характеристике при фиксированном токе I iрад/с. Жесткость естественной механической характеристики β* =(М*0 – М*н)/(ω*0 – ω*н), где М *0 – момент, соответствующий скорости идеального холостого хода; М *0 = 0. Отношение скольжений на естественной и искусственной характеристиках sе/sи = R2/(R2 + R2д.р).
|

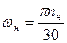 номинальная скорость якоря, рад/с; пн – номинальная частота вращения двигателя, мин-1.
номинальная скорость якоря, рад/с; пн – номинальная частота вращения двигателя, мин-1.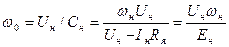 .
. .
. ;
;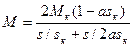 ,
, .
.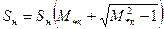 .
. ,
,


