Частотное регулирование скорости асинхронных двигателей
Впервые о влиянии частоты источника питания на работу асинхронного двигателя сообщили Масаивет (1919 г.) и И. Костко (1922 г.). Появление фундаментальной работы акад. М. П. Костенко (1925 г.) положило начало теории частотного управления АД. Наиболее интенсивно развивались эти работы в нашей стране в трудах А. А. Булгакова, Д. А. Завалишина В. А. Прозорова, Ю. А. Сабинина, Б. И. Фираго, М. 3. Хамудханова, В. А. Шубенко и других ученых. Принцип реализации частотного управления АД весьма прост и основан на том, что синхронная скорость машины определяется следующим соотношением: ω0=2π f 1/р, где f 1 - частота источника питания статора. Поэтому, изменяя частоту тока в статоре, можно плавно регулировать скорость вращения ротора в широких пределах. Этот способ регулирования скорости характеризуется в основном потерями скольжения ∆р = Pп s, которые незначительно изменяются при большом диапазоне изменения частоты.
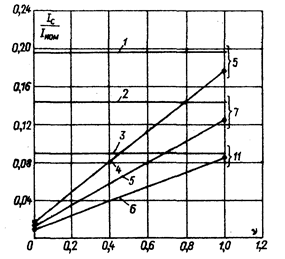
Рис. 1.5. Оценка 5—7—11 гармонических составляющих тока, потребляемого из сети, в приводах постоянного тока с преобразователем напряжения (кри- i2, 3) и переменного тока с преобразователем частоты (кривые 4, 5, 6) В связи с техническим решением в 50-60-е годы проблемы создания надежных и экономичных статических преобразователей частоты на полупроводниковых приборах (транзисторах и тиристорах) частотное регулирование скорости двигателей переменного тока и других его разновидностей получило широкое распространение в промышленном электроприводе. Таким образом, если 20—30 лет назад считалось невозможным реализовать широкое регулирование скорости асинхронного, тем более короткозамкнутого двигателя, то сегодня не существует такой проблемы. Причем по результатам исследований фирмы ABB [1] потери от токов высших гармоник при частотном регулировании асинхронных, короткозамкнутых двигателей оказываются значительно ниже, чем в современных регулируемых приводах с двигателями постоянного тока (рис. 1.5). Схема замещения частотно-управляемого асинхронного привода. Для реализации частотного регулирования скоростями асинхронного двигателя необходимо иметь источник напряжения переменного тока регулируемой частоты. Использование для этих целей синхронных генераторов с регулируемой частотой вращения не оправдывается ни техническими, ни экономическими соображениями. Только при появлении статических полупроводниковых преобразователей возникла реальная возможность создания частотно - регулируемых промышленных электроприводов.
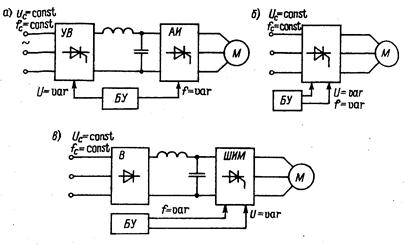
Рис. 1.6. Системы ПЧ -АД: а - с промежуточным звеном постоянного тока ПЧ - АИ - АД; б - с НПЧ; в - с ШИМ преобразователем - ПЧ - ШИМ - АД УВ - управляемый выпрямитель; АИ - автономный инвертор; НПЧ - преобразователь непосредственной связи с сетью; В - нерегулируемый выпрямитель; ШИМ - преобразователь с широтно-импульсной модуляцией; БУ - блок управления; М - асинхронный короткозамкнутый двигатель. В большинстве случаев они являются замкнутыми системами. Но основу их составляют преобразователь частоты и асинхронный двигатель (ПЧ- АД). Напомним, что в современной практике используются преобразователи частоты трех видов: с промежуточным звеном постоянного тока и автономным инвертором тока или напряжения (ПЧ— АИ) (рис. 1.6, а); непосредственные (НПЧ) (рис. 1.6, б) и с широтно-импульсной модуляцией (ПЧ—ШИМ) выпрямленного напряжения (рис. 1.6, в). В первых из них можно регулировать частоту выходного напряжения (тока) независимо от величины ее в сети питания, в НПЧ диапазон регулирования частоты ограничен 3…20 Гц при частоте в сети 50 Гц. В преобразователях с ШИМ частота регулируемого напряжения также не ограничивается, как и в ПЧ - АИ, но гармонический состав токов, потребляемых из сети, существенно лучше (рис. 1.7). На рис. 1.8 представлены зависимости потребления реактивной мощности частотно-регулируемыми приводами. Эти зависимости подтверждают снижение влияния гармонических составляющих токов, потребляемых из сети системой ПЧ - ШИМ - АД. Все эти факторы необходимо учитывать при изучении переходных режимов таких систем привода.
Рис. 1.7. Зависимости тока, потребляемого из сети частотно-регулируемыми приводами систем ПЧ - АИ - АД (кривые 1, 2, 3) и ПЧ - ШИМ - АД (кривые 2, 5,6) при различных видах статической нагрузки
Расчет механических характеристик в системе ПЧ - АД может быть выполнен различными способами. Например, можно составить систему уравнений Горева — Парка и решать ее на каждом интервале проводимости вентилей. При этом следует определять ненулевые начальные условия на границах каждого участка. Таким образом, будут учитываться электромагнитные переходные процессы в системе ПЧ — АД. Установившийся режим работы является стационарно - динамическим. Поэтому момент можно найти как среднее его мгновенных значений за период изменения питающего напряжения.
Рис. 1.8. Зависимости потребляемой реактивной мощности частотно-управляемыми приводами ПЧ - АИ - АД (кривая 1) и ПЧ - ШИМ - АД (кривая 2) при номинальной и 50 %-ной нагрузке.
Для исследования характеристик ПЧ—АД используются схемы замещения, подобные тем, которые применялись ранее. Такой метод исследования механических характеристик системы ПЧ—АД является наиболее простым. На рис. 1.9 изображена эквивалентная схема замещения фазы привода ПЧ - АД при соединении обмоток статора и ротора в звезду и приведенных активных и реактивных составляющих сопротивлений ПЧ к цепи статора. Здесь неизменным остается только эквивалентное, активное сопротивление статорной цепи привода r 1, индуктивные составляющие сопротивлений пропорциональны относительному значению частоты питания α:
Рис. 1.9. Эквивалентная схема замещения частотно-регулируемого привода
В дальнейшем будем использовать абсолютное отклонение угловой скорости ротора ∆ω, относительное Sα и абсолютное β скольжение ротора:
где ω0, ω1 — частота вращения магнитного поля при частоте тока в статоре f ном и f i соответственно; ω—частота вращения ротора. Активная составляющая приведенного сопротивления вторичной цепи обратно пропорциональна относительному скольжению. При составлении эквивалентной схемы, практически, использованы прежние допущения. Выходное напряжение преобразователя (питания статора двигателя) принято синусоидальным и равным
где γ;—относительное значение напряжения первой гармоники питания двигателя. Учет искажений, вносимых несинусоидальной формой напряжения питания, приводит к увеличению потерь в частотно-регулируемом приводе и важен при расчете его энергетических характеристик. Механические характеристики определяются взаимодействием первых гармоник токов и потоков машины. Механическая характеристика системы ПЧ—АД. В соответствии с эквивалентной схемой (рис. 1.9) запишем:
где
то для действующего значения тока во вторичной цепи будем иметь:
де
Подставив в формулу значение I 2', найдем
Момент имеет максимум при таком значении абсолютного скольжения:
Тогда, подставляя значение β;к в М, получаем:
Знак «плюс» определяет величину М к в двигательном, а знак «минус»—в генераторном режимах. Используя Мк, найдем выражение для механической характеристики привода:
где Полученная формула аналогична выражению для механической характеристики асинхронного двигателя, но, естественно, теперь электромагнитный момент, помимо зависимости от скольжения β, является функцией α и γ. Законы оптимального управления системой ПЧ—АД. Электромагнитный момент является основной выходной координатой силового привода. При частотном управлении его значение зависит, от частоты и напряжения переменного тока, прикладываемого к статору машины. Поэтому наличие двух независимых каналов управления дает возможность реализовать в системах ПЧ - АД оптимальное управление. Этот закон установил М.П. Костенко, обосновав его следующим образом. Пусть при регулировании скорости привода должна сохраняться постоянной перегрузочная способность двигателя
Следовательно,
Полученное выражение в абсолютных или относительных единицах представляет собой математическую формулировку оптимального закона частотного управления при λм = const. Таким образом, управляя двигателем при ненасыщенной магнитной системе машины, можно сохранить практически неизменным коэффициент мощности и абсолютное скольжение привода, а его КПД независимым от изменения скорости. В этом и заключается критерий оптимальности закона частотного управления. Виды нагрузки определяют различные формы взаимосвязанного управления напряжением и частотой. При постоянном моменте нагрузки:
При постоянной мощности Р = const
Часто нагрузка зависит от скорости:
Рис. 1.10. Механические характеристики привода ПЧ - АД: а - при постоянном моменте; б - при постоянной мощности; в - при вентиляторной системе нагрузки
При этом виде нагрузки формула (1.18) примет такой вид:
В частности, при «вентиляторной» нагрузке Механические характеристики привода, сохраняющего теоретически постоянство перегрузки двигателя при всех перечисленных видах нагрузки, приведены на рис. 1.10. Однако, как видно из графиков, изображенных пунктирными линиями (рис. 1.10, а), рассчитывая напряжение по формуле (1.18), не удается сохранить постоянство перегрузки двигателя, особенно при постоянном статическом моменте. Это связано с тем, что при уменьшении частоты растет влияние падения напряжения в активном сопротивлении статорной цепи, которое не учитывается при таком управлении в выражении (1.18). Особенно это заметно в приводах малой мощности. Поэтому скорректированная форма оптимального закона частотного управления с компенсацией падения напряжения на статоре при постоянной нагрузке может быть записана в виде
Механические характеристики привода, рассчитанные по формуле (1.19), изображены сплошными линиями на рис. 1.10, а. Оптимальный закон частотного управления при постоянстве перегрузки является не единственным, используемым на практике. Например, часто реализуются другие законы: постоянства магнитного потока машины, минимума потерь и другие. Частотное регулирование с поддержанием постоянства потока тождественно управлению с компенсацией падения напряжения в статорных цепях. При этом асинхронный привод приобретает следующие свойства. · Токи статора, ротора и поток (кроме потерь в стали) остаются неизменными. Поэтому механические характеристиками привода при изменении α перемещаются параллельно по вертикали (рис. 1.10, а).
Рис. 1.11. Асинхронный двигатель при питании от источника тока; а - схема замещения фазы; б - векторная диаграмма.
· При работе с максимальным потоком двигатель имеет жесткую рабочую часть механической характеристики и больший критический момент, чем на естественной характеристике. · При уменьшении нагрузки, поток становится избыточным, что приводит к завышению потерь и неоптимальности этого закона регулирования при переменном моменте нагрузки. При управлении по минимуму потерь создание необходимого момента, пропорционального произведению тока в роторе на поток, осуществляется при равенстве переменных и постоянных потерь, связанных с возбуждением машины (ее магнитным потоком). Такое управление обеспечивает минимум потерь и оптимальность КПД привода. Математическая интерпретация этого закона управления очень сложна. Для того чтобы реализовать принцип частотного управления, необходимо в соответствии с выражениями (1.18) или (1.19) взаимосвязанно управлять напряжением (током) в статоре асинхронной машины при изменении частоты питания. Поэтому в разомкнутых системах ПЧ — АД не удается достичь большого диапазона регулирования скорости, так как в сильной степени проявляется статизм (влияние изменений момента нагрузки) на механические характеристики привода. Например, уже при D = 6:1 статизм достигает 30 %. Кроме того, при снижении скорости может возникать область статической неустойчивости, которая затрудняет практическое использование таких приводов.
|



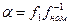 .
.
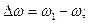
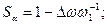
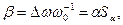
 ,
,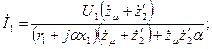

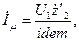
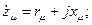
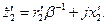 Если пренебречь значением r µ, учитывающим потери в стали, обозначив
Если пренебречь значением r µ, учитывающим потери в стали, обозначив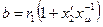 ;
;  ;
;  ;
; 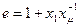 ,
,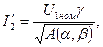
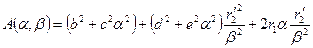 . Вычисляя последовательно электрические потери в роторе и электромагнитный момент, получаем:
. Вычисляя последовательно электрические потери в роторе и электромагнитный момент, получаем: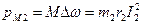 или
или 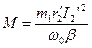 .
.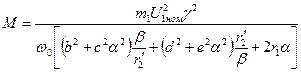 .
.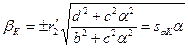 .
.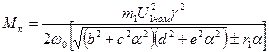 .
. ,
,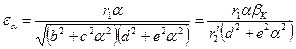 .
.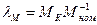 . Тогда, пренебрегая активным падением напряжения в обмотке статора можно записать приближенные равенства:
. Тогда, пренебрегая активным падением напряжения в обмотке статора можно записать приближенные равенства: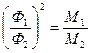 ;
; 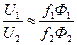 .
. или
или 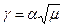 .
. или
или 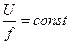 .
.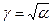 .
. или
или 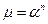 . (1.18)
. (1.18)
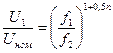 или
или  .
.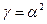 .
. . (1.19)
. (1.19)



