Метод дерева решений

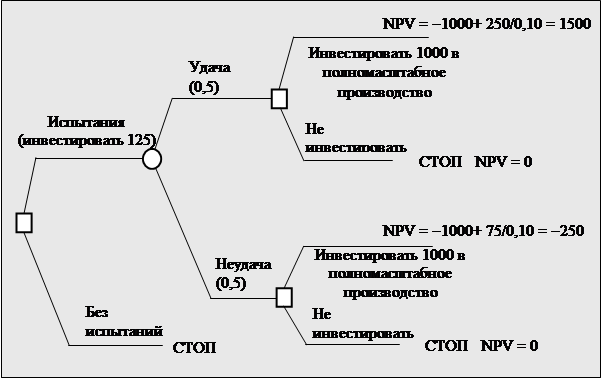
Если финансовый менеджер рассматривает проект как черный ящик, то он, по всей видимости, пытается обдумать только первое решение «принять или отвергнуть» и не учитывает сопутствующие инвестиционные решения, обусловленные первым. Но если последующие инвестиционные решения зависят от исхода сегодняшних, тогда и сегодняшние решения должны приниматься с учетом ваших планов и «погоды» на завтра.

В соответствии с этой посылкой, развитие проекта в целом может быть разбито на ряд последовательных альтернативных этапов и представлено в виде «дерева решений», отражающих альтернативные решения и их результаты.

Для пояснения сказанного рассмотрим примеры, приведенные в учебнике Ричарда Брейли и Стюарта Майерса.

Ученые компании Vegetron вышли с предложением о производстве электрошвабр, и фирма готова начать опытное производство и маркетинговые испытания продукции. Этот этап займет год, а его затраты составят 125 тыс. дол. Руководство считает, что шансы на успех опытного производства и контрольной партии на рынке составляют пятьдесят на пятьдесят. В случае успеха Vegetron построит завод стоимостью 1 млн. дол., который будет приносить ожидаемый годовой посленалоговый денежный поток размером 250 тыс. дол. в течение бесконечного периода времени. В случае неудачи Vegetron не будет продолжать осуществление проекта.

Для осознанного принятия такого решения, следует разобраться с тем, что такое «успех» и «неудача». Линия и параметры успеха уже описаны – это 250 тыс. дол. в течение бесконечного времени после строительства завода. По всей видимости, неудача, – это когда чистая приведенная стоимость проекта будет отрицательной. Конечно, Vegetron могла бы продолжить проект, даже если бы испытания пробной партии закончились неудачей. Давайте, для полноты, предположим, что в этом случае 1 млн. дол. инвестиций приносили бы только 75 тыс. дол. в год.

На рис. 5.5. рассматриваемый проект представлен в виде дерева решений, которое отражает гипотетическую игру Вегетрона с судьбой. Квадратиками отмечены решения Вегетрона, кружочками – решения судьбы. Вегетрон начинает игру с квадратика расположенного слева. Если он решает провести испытания. То судьба бросает кости и решает их исход. Если испытания прошли удачно, а вероятность этого равна 0,5 – тогда фирма должна принять второе решение: инвестировать 1 млн. дол. в проект, дающий чистую приведенную стоимость в размере 1,5 млн. дол. или остановиться. Если испытания прошли неудачно, перед Вегетроном стоит аналогичный выбор, но чистая приведенная стоимость инвестиций составляет – 250 тыс. дол.

Очевидно, что решением второго этапа будет: инвестировать, если испытания закончатся удачно, а если нет – остановиться. Чистая приведенная стоимость отказа от проекта равна нулю, так что дерево решения предлагает простую задачу: следует ли Вегетрону инвестировать сегодня 125 тыс. дол. при 50% вероятности, получить 1500 тыс. дол. в следующем году?

 

 

 

Рис. 5.5. Дерево решений проекта по производству электрошвабр

 

Хочу заметить, что для ответа на этот вопрос уже не достаточно оценки этапа строительства завода как самостоятельного этапа. Необходима оценка NPV всего проекта, включая этап опытного производства и пробного маркетинга – ведь на момент принятия решения этот этап еще не выполнен, и его издержки нельзя считать невозвратными. Авторы примера почему-то не делают этого.

Для оценки эффективности проекта в целом уточним его некоторые детали. Обратим внимание на то, что в нулевой год проекта фирма Вегетрон осуществляет только инвестиции в 125 тыс. дол. По всей видимости, выручка от реализации пробной партии электрошвабр добровольно перечислена в фонд развития международного музея истории сотрудничества американских электрошвабр, и российских электровеников. Понятно, что учет этапа пробного производства и сбыта, отодвинет во времени получение основных доходов. Согласившись с перечислениями в музей, введем в пример уточнения, конкретизирующие реализацию проекта во времени.

Нулевой год: инвестиции в пробное производство маркетинг 125 тыс. дол.

Первый год: реализация пробного маркетинга.

Второй год: строительство завода по полномасштабному производству

С третьего года до бесконечности: серийное производство. Ежегодный приток 250 тыс. дол.

С учетом введенных уточнений, дерево решений проекта будет иметь следующий вид.

 

 

 

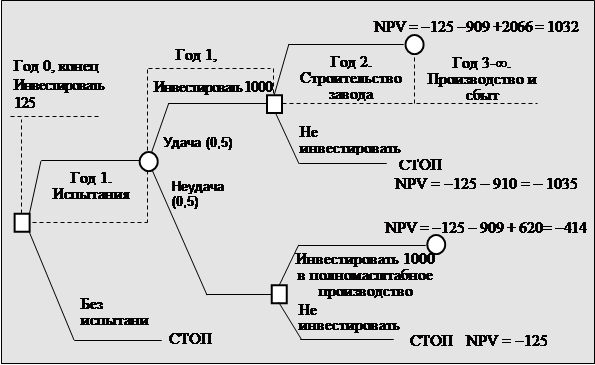
5.6. Уточненное дерево решений проекта по производству электрошвабр

 

Уточненное дерево решений показывает нам реальную альтернативу: отказ от дальнейшего проведения проекта после неудачных испытаний влечет за собой потери в объеме 125 тыс. дол., а принятие проекта, в случае их удачи, – увеличение стоимости фирмы на 1032 тыс. дол. Альтернативные исходы равновероятны. Одним из вариантов сведения этой многокритериальной задачи к одному критерию может быть расчет средневзвешенной по вероятности чистой приведенной стоимости проекта: NPV_СР.ВЗВ. = NPV₁ ´р₁ + NPV₄ ´р₄ = 454 тыс. дол. При таком подходе к интегральной оценке проекта его следует принять. Однако вспомним поговорку о лжи и статистике. Ведь, в случае неудачи, вы потеряете 125 тыс. дол. И если же для вас проигрыш денег значительно более нежелателен, чем желателен выигрыш, то в расчет соответствующей интегральной оценки нужно ввести дополнительные весовые «коэффициенты желательности и нежелательности». Используя механизмы взвешивания, важно понимать, что полученная таким образом величина NPV является оценочной, а не реальной величиной, и при реализации проекта, в зависимости от исхода опытного производства, вы получите значений NPV либо 1032 тыс. дол., либо –125 тыс. дол.

Так что же определенного о проекте может сказать нам этот анализ? Прежде всего, мы существенно «проредили» ветки дерева, оставив всего два пути: в случае удачи пробного производства проект будем делать, а, в случае неудачи – нет. Остальные ветви не рассматриваются. Правда, для данного очень простого примера этот вывод очевиден и без дерева. Однако уже на этом примере можно проиллюстрировать ответ на другой важный вопрос: а стоит ли вообще экспериментировать с пробным производством и сбытом? Может быть, построить завод сразу и не тратить 125 тыс. дол.?

Прежде всего, следует конкретизировать, за что мы платим 125 тыс. дол. По всей видимости, за то, чтобы иметь право отказаться от убыточного проекта, в случае неудачи эксперимента. Покупка права отказа носит название опциона на отказ.

Итак, стоимость опциона на отказ равна 125 тыс. дол.

Второй вопрос, который следует задать в нашем дополнительном анализе, – это вопрос о том, от каких потерь мы себя оберегаем, покупая опцион на отказ. Для ответа на этот вопрос отметим, что, при строительстве завода сразу и неудаче, мы получим приведенные убытки размером в 250 тыс. дол., поскольку в нулевом году осуществим строительство, а, начиная с первого – будем получать 75 тыс. дол. ежегодно (-1000 + 75/0,1 = 250 тыс. дол.). Так стоит ли заплатить 125 тыс., чтобы уберечь себя от убытков в 250 тыс.? В такой постановке ответ очевиден: «да».

Однако тут опять вмешиваются вероятности. Ведь вероятность неудачи всего 50%, и средневзвешенные потери будут равны 125 тыс. дол., то есть в точности стоимости опциона на отказ. В такой постановке вопроса ответ, также очевиден. Платить 125 тыс., чтобы уберечь себя от потерь 125 тыс. не имеет смысла. Вот если бы потери были больше 125 тыс. дол., то тогда «да». Но ведь они и будут больше! Если рыночный спрос будет соответствовать неудачной ветви, то наши потери составят, все-таки, 250 тыс. дол., а это в два раза больше, чем 125 тыс.

Как же здесь быть? На подобный вопрос мы уже отвечали, когда оценивали целесообразность проведения технологического эксперимента проекта «Драндулет». – Однозначного ответа здесь нет. Все зависит от ваших возможностей и склонностей и к риску. Я же хочу отметить, что

 

 

 

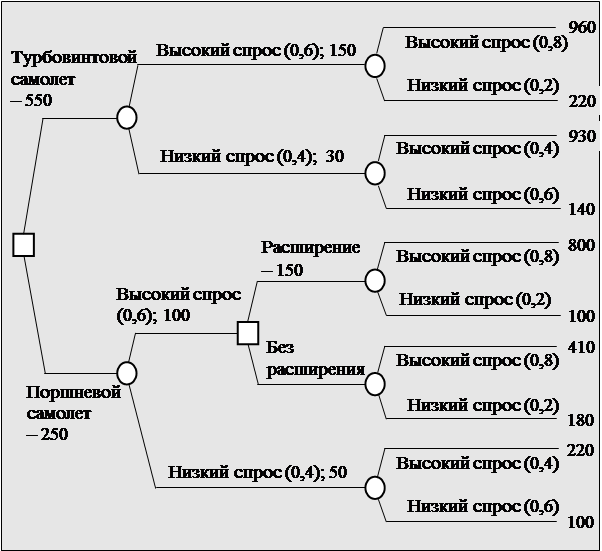
Следующий пример более сложен, но он приближает нас к исследованию реальных ситуаций и раскрывает дополнительные возможности метода «дерева решений».

Руководство компании «Вольный полет», специально созданной для обслуживания служебных перелетов путем разовых предоставлений самолетов временно нуждающимся в них фирмам, решает вопрос о том какой тип самолета лучше приобрести. Альтернативой современному турбовинтовому самолету стоимостью 550 тыс. дол. является поршневой самолет стоимостью 250 тыс. дол. Поршневой самолет имеет меньшую мощность и менее презентабелен. Кроме того, у него устаревшая конструкция, и он, вероятно, быстро износится. Руководство считает, что в следующем году подержанный самолет с поршневым двигателем можно будет приобрести всего лишь за 150 тыс. дол.

В силу того, что спрос прогнозируется лишь предположительно и существует 40% вероятность, что в первый год спрос буден небольшим, естественно возникает идея: почему бы ни начать с одного поршневого самолета и не приобрести другой, если спрос останется высоким? Для этого потребуется только 150 тыс. дол. Если же спрос окажется низким и в первый и во второй год проекта, то компания с одним небольшим и относительно недорогим самолетом будет работать на полную мощность.

Как бы вы поступили в данной ситуации?

Думаю, что «в уме» оценить предложенную ситуацию весьма проблематично. Поэтому построим дерево решений (рис. 5.7).

На рисунке 5.7. квадратиком слева обозначено первоначальное решение компании о реализации проекта и приобретении турбовинтового самолета за 550 тыс. дол. или самолета с поршневым двигателем за 250 тыс. После того как компания принимает это решение, судьба решает проблему спроса в первый год. В скобках проставлена вероятность свершения соответствующего события, а далее – ожидаемые потоки денежных средств.

В конце первого года, если компания имеет поршневой самолет, она должна принять решение: либо расширяться, либо остаться в прежнем состоянии. Это решение отмечено вторым квадратиком.

В это же время в игру опять вступает судьба и выбирает уровень спроса на второй год. В скобках опять приводятся значения вероятностей соответствующих событий, а за ними – ожидаемые денежные потоки.

Важно отметить то обстоятельство, что вероятности той или иной величины спроса второго года зависят от спроса в первом году. Например, если в первый год спрос высокий, тогда существует 80% вероятность, что спрос будет высокий и во второй год. Совместная вероятность высокого спроса в оба периода будет равна 0,6´0,8 = 0,48.

В правой части схемы приведены цифры, характеризующие эффективность соответствующей ветви, которую можно рассматривать как приведенную к данному году стоимость потоков денежных средств, всех последующих лет и этого года.

 

 

 

 

 

Рис. 5.7. Дерево решений проекта компании «Вольный полет»

Проект-менеджер компании должен дать рекомендации руководству относительно приобретения самолета. Очевидно, что принятие сегодняшнего решения зависит от того, что случится в будущем. В этой связи следует проанализировать дерево решений, начиная с правой стороны.

Единственное решение, которое должно принять руководство компании в следующем году, – расширять ли этот бизнес, если высокий спрос будет оправдывать приобретение дополнительного самолета с поршневым двигателем. Если компания решит расширять дело и инвестирует 150 тыс. дол., то получит либо 800 тыс. дол., если спрос останется высоким, либо 100 тыс. дол., если спрос упадет. Таким образом, взвешенный по вероятностям ожидаемый результат будет следующим:

Вероятность высокого спроса ´ исход при высоком спросе +

+ вероятность низкого спроса ´ исход при низком спросе =

= 0,8´800 + 0,2´100 = 660 тыс. дол.

Если альтернативные издержки этого предприятия равны 10%, то чистая приведенная стоимость расширения бизнеса для первого года будет равна:

NPV = –150 + 660/1,10 = 450 тыс. дол.

Если же фирма не станет расширять дело, то ожидаемый результат будет:

Вероятности высокого спроса ´ исход при высоком спросе +

+ вероятность низкого спроса ´ исход при низком спросе =

= 0,8´410 + 0,2´180 = 364 тыс. дол.

Соответствующая приведенная к первому году проекта чистая стоимость будет равна

NPV = 0 + 364/1,10 = 331 тыс. дол.

Очевидно, что расширение выгодно при высоком рыночном спросе.

Теперь, когда мы знаем, что делать компании, если встанет вопрос о расширении, мы можем вернуться к сегодняшнему решению. Если покупается первый поршневой самолет, можно ожидать получения в первом году 550 тыс. дол. при высоком спросе и 185 тыс. дол. при низком. Эти цифры получаются как суммы соответствующих денежных потоков первого года и приведенных к первому году средневзвешенных значений PV потоков последующих лет. Соответствующий фрагмент «дерева» имеет вид рис. 5.8

 

 

Рис. 5.8. Преобразованный фрагмент дерева решений

Чистая, приведенная к началу проекта, стоимость инвестиций в самолет с поршневым двигателем, следовательно, равна:

NPV = – 250 + (0,6´550 + 0,4´185)/1,10 = 117 тыс. дол.

Если же компания купит турбовинтовой самолет, никаких будущих решений анализировать не придется. Для оценки этой ветви дерева достаточно вычислить и продисконтировать соответствующие денежные потоки:

NPV = – 550 + (0,6´150 + 0,4´30)/1,10 +

+[0,6(0,8´960 + 0,2´220) + 0,4(0,4´930 + 0,6´140)]/ (1,100)² =

= – 550 + 102/1,10 + 670/(1,10)² = 96 тыс. дол.

Таким образом, чистая приведенная стоимость инвестиций в самолет с поршневым двигателем равна 117 тыс. дол., а в турбовинтовой самолет 96 тыс. дол. Поршневой самолет являет собой лучший выбор. Однако отметим, что выбор мог бы быть и другим, если бы мы забыли учесть возможность расширения. В этом случае чистая приведенная стоимость инвестиций в поршневой самолет снизилась бы со 117 тыс. дол. до 52 тыс. дол.:

NPV = – 250 + (0,6´100 + 0,4´50)/1,10 +

+[0,6(0,8´410 + 0,2´180) + 0,4(0,4´220 + 0,6´100)]/ (1,100)² =

= – 250 + 80/1,10 + 277/(1,10)² = 52 тыс. дол.

Следовательно, стоимость возможности расширения, или опциона на расширение, составляет: