Шаг 2. Задание вероятностных характеристик переменных

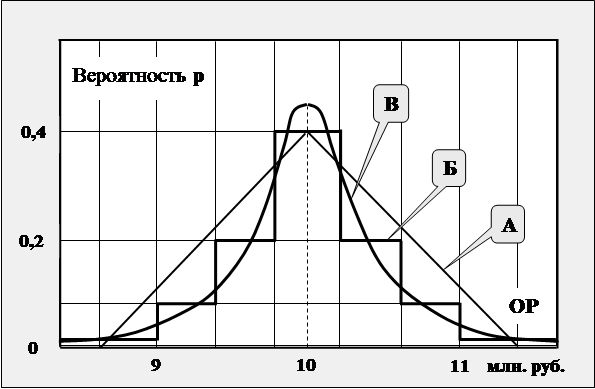
Построив имитационную модель, следует определиться с данными о входных и возмущающих переменных. Суть имитационного моделирования по методу Монте-Карло заключается в том, что по заданным стохастическим характеристикам переменных (тренду и колеблемости) компьютер случайным образом генерирует значение входных и возмущающих переменных и получает соответствующие значения выходных переменных. Проделав достаточное количество таких «опытов» можно получить стохастические характеристики выходных переменных.

Из сказанного ясно, что метод Монте-Карло требует задания входных и возмущающих переменных как случайных величин. Это можно сделать различными путями: в форме генерации случайной выборки из таблицы возможных значений, в аналитической форме, в форме реализации компьютерного генератора случайных чисел из заданного диапазона и т.п. При этом в любом случае нужно знать статистические характеристики случайных величин.

Допустим, что, будучи менеджером проекта, вы поручили отделу маркетинга спрогнозировать объем рынка и его возможные отклонения. Отдел маркетинга сообщил вам, что ожидаемое значение объема рынка равно 10 млн. машин в год, с относительной погрешностью 10%. Для моделирования этого явно не достаточно. Компьютеру «нужно знать», с какой вероятностью значение объема рынка принимает то или иное значение (точнее попадает на тот или иной интервал значений). Это уже значительно сложнее.

Допустим, что в ответ на это замечание, вам нарисовали кривую А рисунка 5.3. Вполне понятно, что возможна ситуация, когда реальное значение емкости рынка будет более 11 млн. руб., или менее 9 млн. руб. Приведенные значения «треугольной» кривой распределения вероятностей исключают такие возможности. В этой связи, вы можете попросить отдел маркетинга уточнить прогноз. Вполне возможно, что, имея опыт работы на рынке автомобилей и проанализировав общеэкономические тенденции, маркетологи дадут более точный прогноз в виде кривой Б рисунка 5.3 и соответствующих ей неравенств

0 £ ôdОРô £ 0,02, р = 0,4;

0,02 <ôdОРô £ 0,06, р = 0,4;

0,06 <ôdОРô £ 0,10, р = 0,15

0,08 <ôdОРô £ ¥, р = 0,05

 

Приведенная гистограмма показывает, что, скорее всего, реально значение емкости рынка как случайная величина имеет нормальное распределение с математическим ожиданием около 10 млн. руб. и среднеквадратическим отклонением около 0,33 млн.

В рассмотренном примере, фактическое значение емкости рынка можно рассматривать как непрерывную случайную величину, кривая распределения вероятностей которой близка к кривой В рисунка 5.3.

Аналогично аналитически или таблично должны быть заданы и остальные входные и возмущающие переменные, (если, конечно, вы их рассматриваете как случайные величины).

 

 

 

 

 

Рис. 5.3. Кривые распределения вероятностей объема рынка

Приведенная гистограмма показывает, что, скорее всего, реально значение емкости рынка как случайная величина имеет нормальное распределение с математическим ожиданием около 10 млн. руб. и среднеквадратическим отклонением около 0,33 млн.

В рассмотренном примере, фактическое значение емкости рынка можно рассматривать как непрерывную случайную величину, кривая распределения вероятностей которой близка к кривой В рисунка 5.3.

Аналогично аналитически или таблично должны быть заданы и остальные входные и возмущающие переменные, (если, конечно, вы их рассматриваете как случайные величины).