Метод Монте-Карло
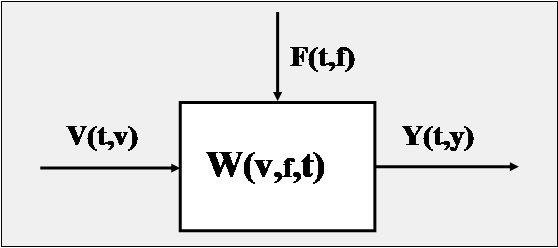
Анализ чувствительности позволяет единовременно оценивать влияние на эффективность проекта изменения только одной переменной. Рассматривая проект при различных сценариях, можно выявить результаты ограниченного числа вероятных сочетаний переменных. Метод Монте-Карло позволяет оценить все возможные комбинации. Для пояснения сказанного, рассмотрим общую модель системного стохастического описания объекта управления (рис. 5.1).
Рис. 5.1. Общая модель системного описания объекта управления С системных позиций, любой объект можно представить как некое устройство, которое преобразует входные векторные переменные V(t,v)в выходные Y(t,y). При этом преобразование и его характеристика W (X,f,t) зависят от возмущающих воздействий со стороны окружающей среды F(f,t) и состояния самого объекта X(x,t). С системным подходом к проблеме финансового управления мы достаточно подробно познакомились в первой части нашего курса. Здесь же, я просто поясню с его помощью метод Монте-Карло. Допустим, что нам известны прогнозные характеристики переменных V, F, и W как случайных функций. То есть, известны зависимости от времени тренда и колеблемости этих величин (ожидаемые значения V и возможный случайный разброс реальных значений относительно ожидаемых). Тогда, построив модель, связывающую V, F, W, и Y, мы могли бы многократно проимитировать процесс реализации проекта преобразования входных переменных V в выходные Y как случайный процесс, с учетом возможных случайных значений F и W, и получить прогноз Y(t,y), с учетом его стохастических характеристик. Это позволило бы нам, например, определить вероятность нахождения выходных величин в заданном диапазоне.
В процессе разработки модели и имитационного моделирования, необходимо понимать и помнить, что все значимые переменные модели рассматриваются как случайные функции. Для напоминания об этом, на рис. 5.1 переменные модели изображены как функции времени (t) и характеристик разброса (v, f). Самыми трудными задачами метода стохастического моделирования являются задачи построения адекватной модели объекта и проекта и получение стохастических характеристик входных, и возмущающих переменных. Так, например, если вместо математической модели, описывающей транспортер, вы заложите в компьютер, математическую модель, описывающую мясорубку, то результаты будут соответствующими. Я специально привел такой пример, поскольку, строго говоря, мясорубкой является любая неадекватная модель процесса. Примерно тоже самое можно сказать и о неточностях в задании стохастических характеристик переменных модели.
.
Для получения более четкого представления о методе Монте-Карло рассмотрим как использовать его для исследования вышеописанного проекта компании «Драндулет».
|