ПРОГРАММИРОВАНИЯ
Математическая формулировка задачи оптимизации часто может быть представлена как задача отыскания наибольшего или наименьшего значения функции нескольких переменных
где функция На независимые переменные
или неравенств:
или же тех и других одновременно. Особые трудности возникают тогда, когда соотношение (2.1), определяющее значение критерия оптимальности для заданной совокупности значений независимых переменных Как правило, решение задач нелинейного программирования может быть найдено только численными методами, поэтому возникает необходимость применения вычислительной техники. В большинстве своем методы нелинейного программирования могут быть охарактеризованы как многошаговые методы или методы последовательного улучшения начального решения. Большинство методов нелинейного программирования используют идею движения в n-мерном пространстве в направлении оптимума. При этом из некоторого исходного или промежуточного состояния
Очевидно, что для случая поиска минимума целевой функции
иначе перевод в состояние Значительное число методов нелинейного программирования в соответствии со способом определения шага 1) градиентные методы; 2) безградиентные методы детерминированного поиска; 3) методы случайного поиска.
|

 (2.1)
(2.1)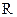 является количественной оценкой представляющего интерес качества объекта оптимизации.
является количественной оценкой представляющего интерес качества объекта оптимизации.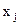
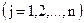 в общем случае можно наложить ограничения в виде равенств:
в общем случае можно наложить ограничения в виде равенств: ,
, 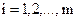 (2.2а)
(2.2а)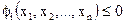 ,
, 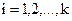 (2.2б)
(2.2б)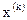 осуществляется переход в следующее состояние
осуществляется переход в следующее состояние 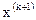 изменением состояния
изменением состояния  , называемую шагом
, называемую шагом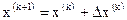 . (2.3)
. (2.3) должно выполняться условие
должно выполняться условие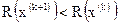 ,
,


