Метод наискорейшего спуска
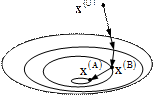
При применении метода градиента на каждом шаге нужно определять значения частных производных оптимизируемой функции по всем независимым переменным. Сокращения объема вычислений можно добиться используя метод наискорейшего спуска. Сущность метода заключается в следующем. После того как в начальной точке будет найден градиент оптимизируемой функции и тем самым определено направление ее наибыстрейшего убывания в указанной точке, в данном направлении делается шаг спуска (рис. 2.2). Если значение функции в результате этого шага уменьшилось, производится очередной шаг в том же направлении, и так до тех пор, пока в этом направлении не будет найден минимум, после чего вычисляется градиент и определяется новое направление наибыстрейшего убывания целевой функции.
Рис. 2.2. Характер движения к оптимуму в методе наискорейшего спуска (–) и методе градиента (∙∙∙∙) В сравнении с методом градиента метод наискорейшего спуска оказывается более выгодным из-за сокращения объема вычислений. Важной особенностью метода наискорейшего спуска является то, что при его применении каждое новое направлении движения к оптимуму ортогонально предшествующему. Это объясняется тем, что движение в одном направлении производится до тех пор, пока направление движения не окажется касательным к какой-либо линии постоянного уровня. В качестве критерия окончания поиска может использоваться то же условие, что и рассмотренное выше, либо условие:
где
Совместное применение условий окончания поиска оправдано в тех случаях, когда оптимизируемая функция имеет резко выраженный минимум.
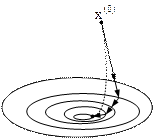
Рис. 2.3. К определению окончания поиска в методе наискорейшего Спуска
|

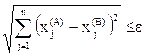 ,
, и
и 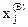 – координаты начальной и конечной точек последнего отрезка спуска. Этот же критерий может использоваться в сочетании с контролем значений целевой функции в точках
– координаты начальной и конечной точек последнего отрезка спуска. Этот же критерий может использоваться в сочетании с контролем значений целевой функции в точках  и
и 
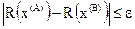 .
.