Пример решения задачи симплексным методом
Требуется найти максимальное значение критерия:
При ограничениях:
Введем дополнительные переменные
С учетом дополнительных переменных коэффициенты
В качестве исходного базисного решения примем решение, соответствующее базису дополнительных переменных, полагая
Значение критерия при этом равно нулю
Соответствующий этому решению исходный базис образован векторами
Небазисные векторы
Разложим небазисный вектор
где Коэффициенты разложения находим из системы уравнений, коэффициентами которой являются компоненты базисных векторов, а правые части представляют компоненты небазисного вектора. Получим
значит Отсюда значение
Проверка условия (3.17) для вектора
Следовательно, переход к новому базисному решению приводит к увеличению критерия оптимальности. Величину приращения определим, выбрав
Минимальное значение имеет величина
Приращение критерия равно
Определим соответствующее базисное решение. В исходном базисе заменяется вектор
Или в векторной форме:
Этому решению соответствуют базисные векторы
Подставляя полученное решение в выражение критерия, найдем
Теперь разложим вектор
Получим систему уравнений
решение которой
Для базисного решения
и условие Величина
Таким образом, в новом базисе исключается вектор
и соответствующее ему базисное решение определяется как
В векторной форме:
Прирост критерия оптимальности при переходе от базисного решения
и новое значение критерия
Для отыскания еще одного базисного решения найдем разложение вектора
Коэффициенты
Вычисляем значение
Следовательно При этом значение
Значит в базисе следует заменить вектор
Соответствующее ему базисное решение
В векторной форме записи:
Прирост критерия оптимальности составляет
Итак, в результате первых трех шагов все векторы первоначального базиса выведены из базиса. Однако, это еще не означает, что уже достигнуто максимальное значение критерия, и процесс поиска нужно прекратить. Необходимо снова попытаться вводить векторы
|

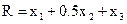 . (1.10)
. (1.10)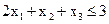 ,
,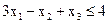 ,
,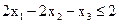 . (1.11)
. (1.11)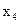 ,
, 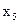 ,
, 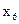 , с помощью которых неравенства (1.11) можно представить в виде равенств
, с помощью которых неравенства (1.11) можно представить в виде равенств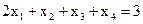 ,
,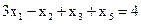 ,
,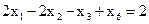 . (1.12)
. (1.12)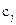 в выражении критерия оптимальности составляют
в выражении критерия оптимальности составляют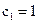 ,
, 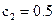 ,
, 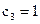 ,
, 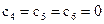 .
. ,
,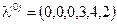 .
. .
.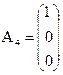 ,
, 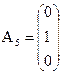 ,
, 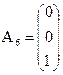 .
.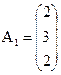 ,
, 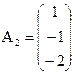 ,
, 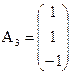 .
.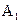 по векторам базиса
по векторам базиса ,
,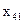 ,
, 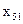 ,
, 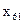 – коэффициент разложения, величины положительные.
– коэффициент разложения, величины положительные.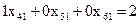 ,
,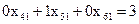 ,
, ,
,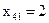 ,
, 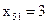 ,
, 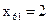 .
.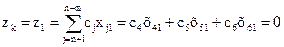 .
.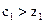 .
.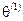 . Для этого найдем величины
. Для этого найдем величины 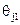
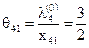 ,
, 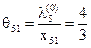 ,
, 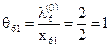 .
.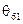 , поэтому примем
, поэтому примем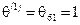 .
. .
.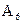 на вектор
на вектор 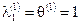 ,
,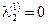 ,
,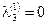 ,
,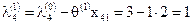 ,
,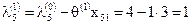 ,
, .
.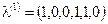 .
.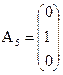 .
.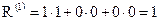 .
.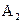 по векторам нового базиса.
по векторам нового базиса.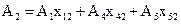 .
.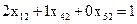 ,
,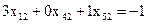 ,
,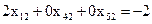 ,
,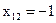 ,
, 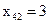 ,
, 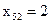 ,
,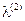 , получим
, получим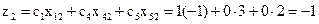
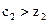 выполняется, следовательно, новое базисное решение вызывает увеличение критерия оптимальности.
выполняется, следовательно, новое базисное решение вызывает увеличение критерия оптимальности. , определяемая как наименьшее положительное отношение
, определяемая как наименьшее положительное отношение 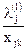 , в данном случае равна
, в данном случае равна .
. и вместо него вводится вектор
и вместо него вводится вектор 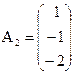 ,
, 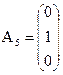
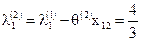 ,
,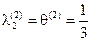 ,
,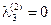 ,
,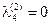 ,
,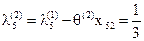 ,
, .
.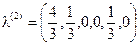 .
.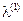 к новому базисному решению
к новому базисному решению 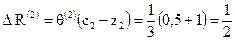
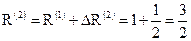 .
.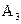 по векторам базиса, соответствующего базисному решению
по векторам базиса, соответствующего базисному решению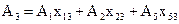 .
.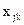 в разложении находим из системы уравнений
в разложении находим из системы уравнений ,
,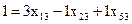 ,
,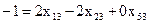 ;
; ,
, 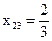 ,
, 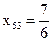 .
.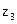
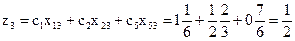 .
.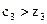 , что означает: новое базисное решение дает большее значение критерия оптимальности.
, что означает: новое базисное решение дает большее значение критерия оптимальности.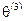 с учетом базисного решения получается равным
с учетом базисного решения получается равным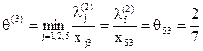
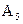 на
на 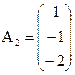 ,
, 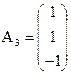 .
.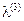
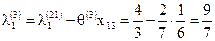 ,
,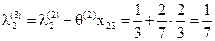 ,
,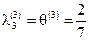 ,
,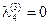 ,
,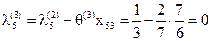 ,
,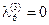 .
.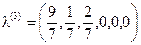 .
.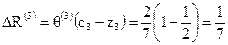 ,
,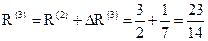 .
.


