ПРИМЕНЕНИЕ СИМПЛЕКСНОГО МЕТОДА В ЗАДАЧАХ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Значительное число планово-производственных задач имеет выражение критерия оптимальности в виде линейной функции от входящих в него переменных. При этом на указанные переменные могут быть также наложены некоторые ограничения в форме линейных равенств или неравенств. Примером подобных задач является задача отыскания такого распределения ограниченного количества сырья между различными производствами, когда общая стоимость получаемой продукции максимальна. Решение этих задач, математическая формулировка которых сводится к требованию максимизации или минимизации критерия оптимальности, заданного в виде линейной функции независимых переменных с линейными ограничениями на них составляет задачу линейного программирования[1,2]. В задачах линейного программирования критерий оптимальности представляется в виде
где На значения переменных
При этом предполагается Будем также считать, что все величины Число ограничений типа равенств Коэффициенты Оптимальным решением задачи линейного программирования, или как еще называют, оптимальным планом является совокупность неотрицательных значений переменных
|

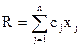 , (1.1)
, (1.1)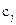
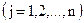 – заданные постоянные коэффициенты, среди которых могут быть и равные нулю.
– заданные постоянные коэффициенты, среди которых могут быть и равные нулю.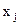
 ,
, 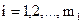 ; (1.2а)
; (1.2а)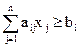 ,
, 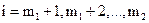 ; (1.2б)
; (1.2б)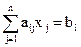 ,
, 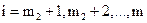 . (1.2в)
. (1.2в)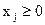
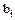 в ограничениях (1.2) отличны от нуля и положительны.
в ограничениях (1.2) отличны от нуля и положительны.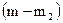 не должно превышать число переменных
не должно превышать число переменных 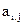 в соотношениях (1.2) принимаются действительными числами, положительными или отрицательными, среди которых могут быть и равные нулю.
в соотношениях (1.2) принимаются действительными числами, положительными или отрицательными, среди которых могут быть и равные нулю.


