Реактора идеального смешения
Рассмотрим задачу минимизации себестоимости продукта реакции в реакторе идеального смешения. Для реакции первого порядка найти оптимальные условия, минимизирующие себестоимость получаемого продукта Р из исходного продукта А, определяемую с учетом затрат на сырье и амортизацию реактора. Скорости образования компонентов А и Р имеют вид:
где
Критерий оптимальности, значение которого необходимо минимизировать, в данном случае имеет вид:
где Минимизация критерия оптимальности R производится выбором оптимальных значений температуры в реакторе Т и времени пребывания реагентов в реакторе
|
,
.
, 
– константы скорости реакций, связаны с температурой реакции уравнением Аррениуса
,
,
,
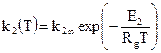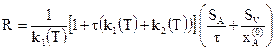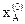– концентрация сырья в реакционной смеси, подаваемой в реактор; 
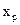– концентрация продукта на выходе реактора; 
– стоимость исходного сырья;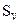 
– стоимость единицы объема реактора, исчисляемая с учетом его амортизации; V – объем реактора; 
– скорость потока сырья, поступающего в зону идеального смешении; 
, 
– предэкспоненциальные множители;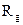 
– универсальная газовая постоянная; Т – температура в реакционной зоне; 
, 
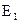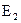– энергия активации компонентов.
.
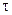