1. Изучить принцип максимума.
2. В случае интегральной формы записи функционала ввести новую переменную с нулевым начальным условием.
3. Составить функцию Гамильтона согласно варианту (табл. 3.1).
4. Определить систему сопряженных функций и граничных условий.
5. Составить условие максимума функции Гамильтона.
Таблица 3.1
Варианты задания III
| Варианты 1, 11.
| Варианты 2, 12.
|
Дана система
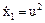 , , 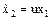 .
Необходимо найти управление u,
минимизирующее функционал .
Необходимо найти управление u,
минимизирующее функционал
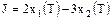 . .
| Дана система
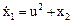 , , 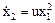 .
Необходимо найти управление u,
максимизирующее функционал .
Необходимо найти управление u,
максимизирующее функционал
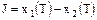 . .
|
| Варианты 3, 13.
| Варианты 4, 14.
|
Процесс описывается уравнением
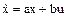 , ,
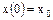 , , 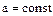 , , 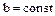 .
Найти управление u, минимизирующее функционал .
Найти управление u, минимизирующее функционал 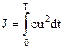 . .
| Процесс описывается уравнением
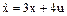 , ,
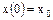 .
Найти управление u, минимизирующее функционал .
Найти управление u, минимизирующее функционал 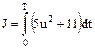 . .
|
| Варианты 5, 15.
| Варианты 6, 16.
|
Дана система
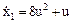 , , 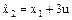 .
Необходимо найти управление u,
минимизирующее функционал .
Необходимо найти управление u,
минимизирующее функционал
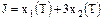 . .
| Дана система
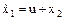 , , 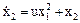 .
Необходимо найти управление u,
максимизирующее функционал .
Необходимо найти управление u,
максимизирующее функционал
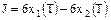 . .
|
| Варианты 7, 17.
| Варианты 8, 18.
|
Процесс описывается уравнением
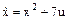 , , 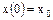 .
Найти управление u, минимизирующее функционал .
Найти управление u, минимизирующее функционал 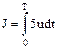 . .
| Процесс описывается уравнением
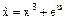 , , 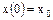 .
Найти управление u, минимизирующее функционал .
Найти управление u, минимизирующее функционал 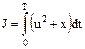 . .
|
| Варианты 9, 19.
| Варианты 10, 20.
|
Дана система
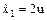 , , 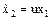 , , 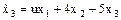 .
Необходимо найти управление u,
минимизирующее функционал .
Необходимо найти управление u,
минимизирующее функционал
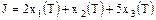 . .
| Дана система
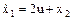 , , 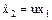 , , 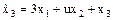 .
Необходимо найти управление u,
минимизирующее функционал .
Необходимо найти управление u,
минимизирующее функционал
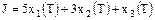 . .
|

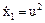 ,
, 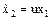 .
Необходимо найти управление u,
минимизирующее функционал
.
Необходимо найти управление u,
минимизирующее функционал
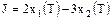 .
.
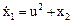 ,
, 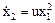 .
Необходимо найти управление u,
максимизирующее функционал
.
Необходимо найти управление u,
максимизирующее функционал
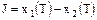 .
.
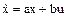 ,
,
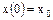 ,
, 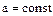 ,
, 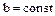 .
Найти управление u, минимизирующее функционал
.
Найти управление u, минимизирующее функционал 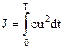 .
.
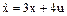 ,
,
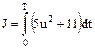 .
.
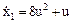 ,
, 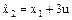 .
Необходимо найти управление u,
минимизирующее функционал
.
Необходимо найти управление u,
минимизирующее функционал
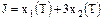 .
.
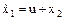 ,
, 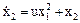 .
Необходимо найти управление u,
максимизирующее функционал
.
Необходимо найти управление u,
максимизирующее функционал
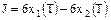 .
.
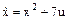 ,
, 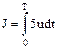 .
.
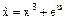 ,
, 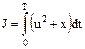 .
.
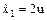 ,
, 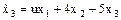 .
Необходимо найти управление u,
минимизирующее функционал
.
Необходимо найти управление u,
минимизирующее функционал
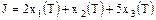 .
.
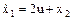 ,
, 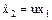 ,
, 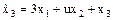 .
Необходимо найти управление u,
минимизирующее функционал
.
Необходимо найти управление u,
минимизирующее функционал
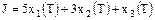 .
.



