Задание с выбором одного верного ответа

Из предложенных вариантов ответов выберите только один верный вариант.

2.1. Функция Гамильтона имеет вид:

1) ;

2) ;

3) ;

4) .

2.2. Какими свойствами обладает Функция Гамильтона вдоль оптимальной траектории процесса:

1) функция непрерывна и постоянна;

2) функция непрерывна;

3) функция постоянна;

4) функция имеет точки разрыва.

2.3. Модуль градиента функции определяется выражением:

1) ;

2) ;

3) ;

4) .

2.4. Необходимое и достаточное условие существования решения основной задачи управления:

1) ;

2) ;

3) ;

4) .

2.5. Критерий оптимальности в задачах линейного программирования имеет вид:

1) ;

2) ;

3) ;

4) .

2.6. Типичной задачей линейного программирования является:

1) задача поиска экстремума нелинейной функции;

2) задача на условный экстремум;

3) транспортная задача;

4) вариационная задача.

2.7. Дайте определение функционала

1) функционал – это переменная величина, которая зависит от выбора функции (или кривой);

2) функционал – это постоянная величина;

3) функционал – это функция;

4) функционал – это независимая переменная величина.

2.8. Необходимым условием экстремума функции многих переменных является:

1) равенство нулю частных производных функции второго порядка;

2) равенство нулю градиента функции;

3) равенство нулю первой вариации;

4) максимум функции Гамильтона.

2.9. В основе динамического программирования используется:

1) принцип оптимальности Бэллмана;

2) принцип максимума;

3) уравнение Эйлера;

4) симплексный метод.

2.10. Математическая формулировка принципа оптимальности для дискретных процессов имеет вид:

1) ;

2) ;

3) ;

4) .

Контрольные вопросы

1. Сформулируйте задачу линейного программирования в общем виде.

2. Что такое оптимальный план?

3. Как осуществляется сведение задачи с ограничениями типа неравенств к задаче с ограничениями типа равенств?

4. В каких задачах используется симплексный метод?

5. Алгоритм симплекного метода.

6. Сформулируйте задачу нелинейного программирования в общем виде.

7. Назовите основные методы решения задачи нелинейного программирования.

8. Основные достоинства и недостатки градиентных, безградиентных методов, методов случайного поиска и сканирования.

9. Алгоритмы решения задачи методами наискорейшего спуска, сканирования, случайных направлений.

10. В чем состоит отличие метода наискорейшего спуска от метода градиента?

11. Объясните основные особенности методов случайного поиска и способы получения случайных чисел.

12. Назовите методы решения задач с ограничениями типа равенств и неравенств.

13. Формулировка принципа максимума.

14. В какихзадачах следует применять принцип максимума?

15. Сформулируйте задачу со свободным правым концом.

16. Для каких систем принцип максимума является необходимым и достаточным условием оптимальности.

17. Что такое многостадийный процесс?

18. Формулировка принципа Бэллмана.

19. Формулировка основной задачи управления.

20. Эквивалентное преобразование задачи.

21. Постановка задачи векторной оптимизации.

22. Сущность метода Парето.
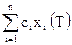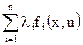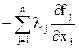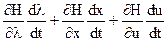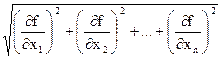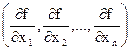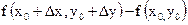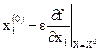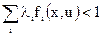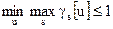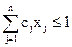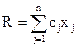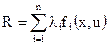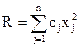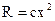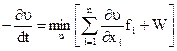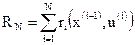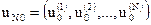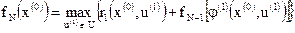