Большое место среди циклов с неизвестным числом повторений занимают циклы, когда в процессе повторения тела цикла образуются последовательность значений 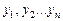 сходятся к некоторому пределу
сходятся к некоторому пределу  , т.е.
, т.е.
 .
.
Каждое новое значение 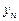 в такой последовательности определяется с учетом предыдущего
в такой последовательности определяется с учетом предыдущего  и является по сравнению с ним более точным приближением к некоторому результату (пределу)
и является по сравнению с ним более точным приближением к некоторому результату (пределу)  . Циклы, реализующие такую последовательность приближений (итерации), называют итерационными.
. Циклы, реализующие такую последовательность приближений (итерации), называют итерационными.
В итерационных циклах условие продолжения цикла основывается на свойстве безграничного приближения значения 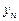 к пределу, а при увеличении
к пределу, а при увеличении 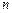 . Итерационный цикл заканчивают, то есть результат отождествляют со значением
. Итерационный цикл заканчивают, то есть результат отождествляют со значением 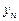 , считается, что
, считается, что 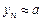 , если для некоторого значения
, если для некоторого значения 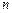 выполняется условие:
выполняется условие:
 ,
,
где 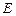 – допустимая погрешность вычисления результата.
– допустимая погрешность вычисления результата.
Типичным примером итерационного цикла может служить задача вычисления суммы бесконечного ряда. Понятие суммы связано с понятием сходимости бесконечного ряда. Бесконечный ряд значений 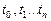 называется сходящимся, если сумма
называется сходящимся, если сумма  его первых
его первых  слагаемых при беспредельном возрастании
слагаемых при беспредельном возрастании 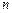 стремится к некоторому пределу
стремится к некоторому пределу  , который и называется суммой ряда, т.е.
, который и называется суммой ряда, т.е.
 ,
, 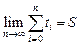 .
.
Общий член 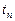 сходящегося ряда при этом стремится к нулю, т.е.
сходящегося ряда при этом стремится к нулю, т.е.
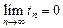 ,
, 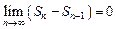 .
.
Следовательно, последовательность 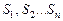 является искомой последовательностью значений и определяет следующие условие окончания суммирования:
является искомой последовательностью значений и определяет следующие условие окончания суммирования:
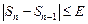 или
или  .
.
Пример 14. Вычислить с погрешностью 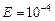 значение функции
значение функции 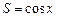 , используя разложение косинуса в ряд:
, используя разложение косинуса в ряд:
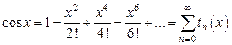 , где
, где 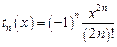 .
.
Аналогично вычислению конечной суммы в данном случае необходимо, во-первых, определить значение очередного слагаемого 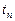 , во-вторых, осуществлять накопление суммы по итерационной формуле:
, во-вторых, осуществлять накопление суммы по итерационной формуле:  .
.
Для определения 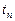 в данном примере из-за наличия факториала целесообразно использовать не прямое вычисление по общей формуле, а рекурентное соотношение:
в данном примере из-за наличия факториала целесообразно использовать не прямое вычисление по общей формуле, а рекурентное соотношение:
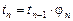
Подставим в формулу для  вместо
вместо 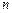 величину
величину  :
:
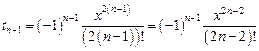
Определим сомножитель 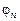 :
:
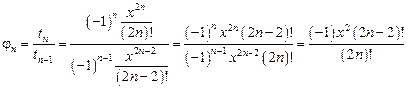 .
.
Т.к. 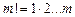 , то
, то
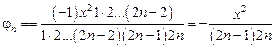 .
.
Начальное значение  находится подстановкой
находится подстановкой  в формулу для
в формулу для  .
.
Т.к. надобности в запоминании значений всех слагаемых 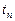 и промежуточных сумм
и промежуточных сумм  нет, то в программе использованы простые переменные:
нет, то в программе использованы простые переменные:
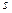 – очередное значение суммы ряда;
– очередное значение суммы ряда;
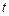 – очередное значение члена ряда;
– очередное значение члена ряда;
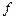 – очередное значение сомножителя
– очередное значение сомножителя 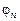 .
.
Алгоритм решения задачи выглядит следующим образом:
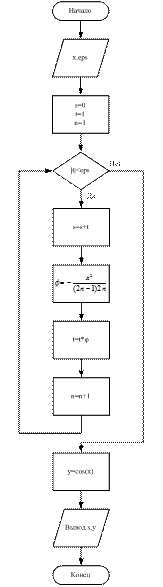
PROGRAM PR14;
VAR n: INTEGER;
eps, s, t, f, x, y: REAL;
BEGIN
READ (x, eps);
s:= 0;
t:= 1;
n:= 1;
WHILE ABS(t)>eps DO
BEGIN
s:= s+t;
f:= -SQR(x)/(2*n*(2*n-1));
t:= t*f;
n:= n+1;
END;
y:= COS(x);
WRITELN (’s=’,s,’y=’,y);
END.
Для проверки полученного результата осуществляется вызов стандартной функции COS(x), значение которой присваивается переменной 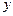 . Для организации цикла по накоплению суммы используется оператор цикла с предусловием, в котором условие
. Для организации цикла по накоплению суммы используется оператор цикла с предусловием, в котором условие  является условием продолжения цикла. Нужно отметить, то что, общий член ряда проверять с погрешностью
является условием продолжения цикла. Нужно отметить, то что, общий член ряда проверять с погрешностью 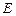 можно только в том случае, если предел
можно только в том случае, если предел 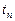 стремится к нулю, в противном случае условием окончания цикла должна быть
стремится к нулю, в противном случае условием окончания цикла должна быть 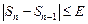 разность предыдущего и последующего значения суммы, сравниваемая с
разность предыдущего и последующего значения суммы, сравниваемая с 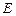 .
.
Итерационный цикл используется для решения алгебраических и нелинейных уравнений. Нахождение корня уравнения вида  осуществляется в два этапа.
осуществляется в два этапа.
На первом этапе – этапе локализации корня – определяется отрезок  , в пределах которого находится один и только один корень уравнения. Одним из способов локализации корня (корней) является построение грубого графика функции
, в пределах которого находится один и только один корень уравнения. Одним из способов локализации корня (корней) является построение грубого графика функции  и определение на этом графике отрезка
и определение на этом графике отрезка  содержащего только один корень. На втором этапе – этапе уточнения корня - ведется поиск корня с заданной степенью точности при помощи некоторого итерационного алгоритма.
содержащего только один корень. На втором этапе – этапе уточнения корня - ведется поиск корня с заданной степенью точности при помощи некоторого итерационного алгоритма.
Наиболее простым методом уточнения корня является метод итераций, заключающийся в следующем: исходное уравнение  , где
, где  непрерывная функция на отрезке
непрерывная функция на отрезке  , заменяют эквивалентным уравнением вида
, заменяют эквивалентным уравнением вида 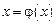 и, зная начальное приближение корня
и, зная начальное приближение корня  каждое следующее, находят по формуле:
каждое следующее, находят по формуле: 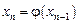 . Вычисления повторяют до тех пор, пока не выполнится условие
. Вычисления повторяют до тех пор, пока не выполнится условие 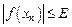 , где
, где 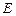 – заданная погрешность вычислений.
– заданная погрешность вычислений.
Пример 15. Определить корень уравнения 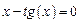 c погрешностью
c погрешностью 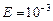 , при начальном значении корня
, при начальном значении корня  .
.
Преобразуем исходное уравнение следующим образом: 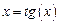 , тогда
, тогда 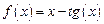 ;
; 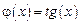 .
.
Для определения  удобно использовать следующие графические построения: построить графики функций
удобно использовать следующие графические построения: построить графики функций  . Точки пересечения этих графиков будут корнями исходного уравнения
. Точки пересечения этих графиков будут корнями исходного уравнения  . На графике выделить приближенные отрезки
. На графике выделить приближенные отрезки  локализации каждого корня. В качестве
локализации каждого корня. В качестве  можно взять любую точку отрезка.
можно взять любую точку отрезка.
Алгоритм уточнения корня по методу итераций:
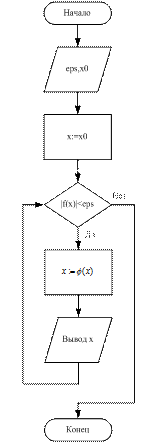
PROGRAM PR15;
VAR eps, x, x0: REAL;
BEGIN
READ (eps,x0);
WRITELN (’исходные данные’);
WRITELN (’ eps=’,eps, ’x0=’, x0);
x:=x0;
WHILE ABS(x-SIN(x)/COS(x))>eps DO BEGIN
x:= SIN(x)/COS(x);
WRITELN (’ x=’,x);
END;
END.
Пример 16. Вычислить интеграл 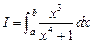 по формуле прямоугольников:
по формуле прямоугольников:  , где
, где 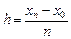 – шаг интегрирования;
– шаг интегрирования;
 – начальное значение интервала интегрирования;
– начальное значение интервала интегрирования;
 – конечное значение интервала интегрирования;
– конечное значение интервала интегрирования;
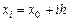 – текущее значение
– текущее значение  ;
;
 – подынтегральная функция.
– подынтегральная функция.

PROGRAM PR16;
VAR a, b, e: REAL;
h, y, y0, fa, fb: REAL;
n, i: INTEGER;
BEGIN
WRITELN (’ введите a,b,n,e);
READ (a, b, n, e);
y:= 0;
REPEAT
y0:= y;
n:= n*2;
fa:= a*a*a/(SQR(SQR(a))+1);
fb:= b*b*b/(SQR(SQR(b))+1);
y:= (fa+fb)/2;
h:= (b-a)/n;
FOR i:=1 TO n-1 DO BEGIN
x:= a+i*h;
y:= y+x*x*x/(SQR(SQR(x))+1);
END;
y:= y*h;
UNTIL ABS (y-y0)<=e;
WRITELN (y);
END.

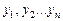 сходятся к некоторому пределу
сходятся к некоторому пределу  , т.е.
, т.е. .
.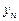 в такой последовательности определяется с учетом предыдущего
в такой последовательности определяется с учетом предыдущего  и является по сравнению с ним более точным приближением к некоторому результату (пределу)
и является по сравнению с ним более точным приближением к некоторому результату (пределу) 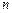 . Итерационный цикл заканчивают, то есть результат отождествляют со значением
. Итерационный цикл заканчивают, то есть результат отождествляют со значением 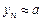 , если для некоторого значения
, если для некоторого значения  ,
,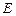 – допустимая погрешность вычисления результата.
– допустимая погрешность вычисления результата.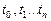 называется сходящимся, если сумма
называется сходящимся, если сумма  его первых
его первых  слагаемых при беспредельном возрастании
слагаемых при беспредельном возрастании  , который и называется суммой ряда, т.е.
, который и называется суммой ряда, т.е. ,
, 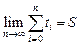 .
.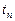 сходящегося ряда при этом стремится к нулю, т.е.
сходящегося ряда при этом стремится к нулю, т.е.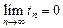 ,
, 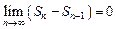 .
.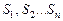 является искомой последовательностью значений и определяет следующие условие окончания суммирования:
является искомой последовательностью значений и определяет следующие условие окончания суммирования: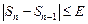 или
или  .
.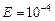 значение функции
значение функции 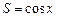 , используя разложение косинуса в ряд:
, используя разложение косинуса в ряд: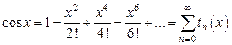 , где
, где 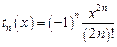 .
. .
.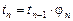
 вместо
вместо  :
: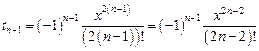
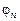 :
: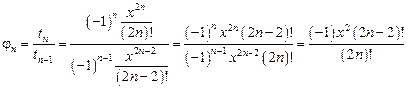 .
.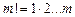 , то
, то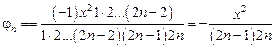 .
. находится подстановкой
находится подстановкой  в формулу для
в формулу для  нет, то в программе использованы простые переменные:
нет, то в программе использованы простые переменные: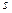 – очередное значение суммы ряда;
– очередное значение суммы ряда;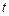 – очередное значение члена ряда;
– очередное значение члена ряда;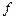 – очередное значение сомножителя
– очередное значение сомножителя 
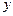 . Для организации цикла по накоплению суммы используется оператор цикла с предусловием, в котором условие
. Для организации цикла по накоплению суммы используется оператор цикла с предусловием, в котором условие  является условием продолжения цикла. Нужно отметить, то что, общий член ряда проверять с погрешностью
является условием продолжения цикла. Нужно отметить, то что, общий член ряда проверять с погрешностью  осуществляется в два этапа.
осуществляется в два этапа. , в пределах которого находится один и только один корень уравнения. Одним из способов локализации корня (корней) является построение грубого графика функции
, в пределах которого находится один и только один корень уравнения. Одним из способов локализации корня (корней) является построение грубого графика функции  и определение на этом графике отрезка
и определение на этом графике отрезка 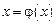 и, зная начальное приближение корня
и, зная начальное приближение корня  каждое следующее, находят по формуле:
каждое следующее, находят по формуле: 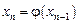 . Вычисления повторяют до тех пор, пока не выполнится условие
. Вычисления повторяют до тех пор, пока не выполнится условие 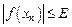 , где
, где 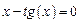 c погрешностью
c погрешностью 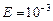 , при начальном значении корня
, при начальном значении корня  .
.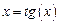 , тогда
, тогда 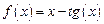 ;
; 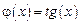 .
. удобно использовать следующие графические построения: построить графики функций
удобно использовать следующие графические построения: построить графики функций  . Точки пересечения этих графиков будут корнями исходного уравнения
. Точки пересечения этих графиков будут корнями исходного уравнения 
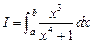 по формуле прямоугольников:
по формуле прямоугольников:  , где
, где 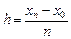 – шаг интегрирования;
– шаг интегрирования; – начальное значение интервала интегрирования;
– начальное значение интервала интегрирования; – конечное значение интервала интегрирования;
– конечное значение интервала интегрирования;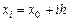 – текущее значение
– текущее значение  ;
;




