Трехмерный кристалл
В идеальном кристалле атомы периодически расположены в пространстве. Такое расположение означает, что при смещении кристаллической решетки на вектор
где a 1, a 2, a 3 – векторы периодов идентичности решетки по трем произвольным направлениям, а n 1, n 2, n 3 – произвольные целые числа, кристалл совмещается сам с собой. Из этого следует, что точка, имеющая радиус-вектор r и точка, имеющая радиус-вектор r + a n физически эквивалентны между собой, поэтому потенциальное поле кристалла
также периодически повторяется в кристаллической решетке. Соотношение (2) выражает условие периодичности потенциального поля кристалла. В кристаллическом поле волновая функция электрона Ψ;(r) (если она не вырождена) может отличаться от волновой функции в Ψ;(r + a n) только постоянным множителем
Но из условия нормировки волновой функции следует, что
поэтому можно положить, что
т.к.
В результате, имеем:
где
- также периодическая функция. Т.о., стационарная волновая функция электрона в периодическом поле кристалла зависит от волнового вектора k и имеет вид:
где множитель ei kr представляет собой плоскую волну, бегущую в направлении вектора k, а U k (r) – некая периодическая координатная функция в выделенном направлении волнового числа. Соответственно, решением уравнения Шредингера для электрона в периодическом поле кристалла является бегущая плоская волна в выделенном направлении, модулированная с периодичностью решетки, а энергия электрона зависит от волнового вектора k. Граничные условия задачи накладывают дополнительные ограничения на возможные значения вектора k. Можно предполагать, что условия на границах кристалла с размерами, существенно превышающими размер элементарной ячейки, не отразятся на его физических свойствах. Наиболее удобным представлением в этом случае являются циклические условия Борна-Кармана. Пусть кристалл имеет форму параллелепипеда с размерами по осям x, y, z соответствующими Lx, Ly, Lz. Для кубической решетки с параметром a соответствующие размеры равняются
где Nx, Ny, Nz – число атомов, укладывающихся на соответствующих ребрах кристалла. Потребуем, чтобы волновая функция Ψ; имела на противоположных гранях параллелепипеда одно и то же значение
Учитывая вид волновой функции для кристаллов, получаем:
Для выполнения условия (12) необходимо принять
Это равенство выполняется, если показатель экспоненты есть целое число, умноженное на 2π i, т.е.
где n 1=0, ±1, ±2, …; n 2=0, ±1, ±2, …; n 3=0, ±1, ±2 …. Т.о. компоненты волнового вектора k изменяется не непрерывно, а принимают ряд дискретных значений. В соответствии с этим оказывается квантованной и энергия электронов в разрешенной зоне. С учетом значений волнового вектора k можно записать волновую функцию электрона в периодическом потенциальном поле кристалла. В одномерном случае волновую функцию электрона можно записать в виде линейной комбинации атомных волновых функций Ψg
где применяется теорема Блоха и ag = R, где R – радиус-вектор, g – номер атомного узла, т.е. целое число, а Lx = aNx. Из (15) видно, что волновая функция при n 1=± Nx будет Ψg и совпадает с волновой функцией при n 1=±1 и т.д. Это означает, что компоненты kx имеют Nx значений, соответствующие различным n 1. При этом n 1 могут принимать 0, 1, 2 … (Nx -1), т.к. E (k)=- E (k), т.е. n 1 меняется только в пределах
Аналогично
где kx, ky, kz принимают соответственно Nx, Ny, Nz различных значений. Следовательно, в разрешенной зоне кристалла имеется всего N = NxNyNz =(LxLyLz)/ a 3 различных энергетических состояний (энергетических уровней), соответствующих различным k, равное числу элементарных ячеек в кристалле. Состояние электрона в атоме характеризуется главным квантовым числом, азимутальным квантовым числом l, магнитным квантовым числом m и спиновой ориентацией sz. Состояние электрона в кристалле согласно принципу Паули также должно описываться четырьмя квантовыми числами. Как следует из (П17), тремя квантовыми числами являются проекции волнового вектора kx, ky, kz, а четвертым квантовым числом должно быть sz, которое принимает только два значения: +1/2 и -1/2 (в терминах ћ). Это означает, что в состоянии (kx,ky,kz) может быть не более двух электронов. Но набор (kx,ky,kz) определяет энергию электрона E (k) для рассматриваемой зоны. Следовательно, на каждом энергетическом уровне зоны, который определяется волновым вектором k в соответствии с принципом Паули на этом уровне может находится не более двух электронов с противоположно направленными спинами. Т.о., в простой энергетической зоне, возникшей из невырожденного атомного уровня, имеется 2 N квантовых состояний, соответствующих N энергетическим уровням и в зоне может быть не более 2 N электронов. Если зона g -кратно вырождена, то в ней может быть 2 gN электронов. Число квантовых состояний в зоне равно общему числу мест на уровнях изолированных атомов, из которых образовались эти зоны, т.е. имеет место сохранение числа состояний при образовании кристалла из атомов. Поэтому в энергетической зоне кристалла имеется N энергетических состояний, которым соответствуют значения компонент волнового вектора
и компонент квазиимпульса
где i = x, y, z, а j =1, 2, 3. Для кристалла с простой кубической решеткой изменение компонент волнового числа и импульса лежит в пределах
Этим значениям квазиимпульса в системе координат (px, py, pz), будет соответствовать некоторая область, построенная вокруг начала координат и содержащая все возможные состояния электронов. Эта область называется первой, или основной, зоной Бриллюэна. Для кристалла с простой кубической решеткой первая зона Бриллюэна для кристалла с кубической решеткой также является кубом, объем которого
В k -пространстве первая зона Бриллюэна для кристалла с кубической решеткой также является кубом, объем которого
Первую зону Бриллюэна можно разбить на элементарные кубические ячейки объемом
где V = L 3= a 3 NxNyNz = a 3 N – объем кристалла, а N = NxNyNz – полное число элементарных ячеек в кристалле. Поскольку объем первой зоны Бриллюэна для кристаллов с простой кубической решетки равен (h / a)3, а объем элементарной ячейки равен h 3/ a 3 N, то число элементарных ячеек в ней составляет N, т.е. равно количеству энергетических состояний в зоне. Но в энергетической зоне могут располагаться 2 N электронов, а в ее каждой ячейке может находиться только два электрона с противоположно направленными спинами. Пусть в кристалле единичного объема в интервале энергий от E до E + dE имеется dz квантовых состояний (с учетом спина). Можно обозначить через N (E) плотность состояний, т.е. число квантовых состояний в единичном интервале энергии для единичного объема кристалла как
Если вероятность заполнения состояний с энергией E равна f (E, T), то число электронов dn, находящихся в состояниях dz составляет величину
Соответственно полное число электронов, для которых возможный интервал энергии лежит в пределах от E 1 до E 2, будет равно:
Энергия электронов у дна зоны проводимости может быть записана в виде
где Ec = E (p 0) – энергия электронов у дна зоны проводимости, m * - эффективная масса электрона. Если выделить шаровой, заключенный между двумя изоэнергетическими поверхностями, соответствующими E (p)= const и E (p)+ dE = const, то объем этого слоя составит величину
где p =I p I. Объем элементарной ячейки зоны Бриллюэна кристалла единичного объема в p -пространстве равен h 3. В каждой ячейке могут находиться два электрона с противоположно направленными спинами. Поэтому число состояний в объеме dV p равно:
Используя равенство (П26) имеем:
и
Подставив равенства (27), (29) и (30) в (23) получается выражение для плотности электронных квантовых состояний у дна зоны проводимости, обладающей сферической симметрией:
Совершенно аналогично, зависимость энергии дырок от их импульса вблизи потолка валентной зоны имеет вид
где Ev – энергия дырки у потолка валентной зоны, mp * - эффективная масса дырок. Совершенно аналогично, (31) плотность энергетических состояний дырок вблизи потолка валентной зоны имеет вид:
рис.1. Нормированная плотность электронных состояний трехмерного кристалла.
|

 , (1)
, (1) (2)
(2) . (3)
. (3) , (4)
, (4) ,(5)
,(5) .(6)
.(6) , (7)
, (7) (8)
(8) , (9)
, (9) , (10)
, (10) . (11)
. (11) . (12)
. (12) . (13)
. (13)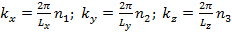 , (14)
, (14) , (15)
, (15) или
или  . (16)
. (16) , (17)
, (17) (17)
(17) , (18)
, (18)
 . (19)
. (19) . (20)
. (20) . (21)
. (21)
 , (22)
, (22) . (23)
. (23) . (24)
. (24) . (25)
. (25) , (26)
, (26) , (27)
, (27) . (28)
. (28) (29)
(29) . (30)
. (30) . (31)
. (31) , (32)
, (32) . (33)
. (33)



