Двумерный кристалл
Двумерная (2D) плотность состояний должна отражать квантовые свойства электронного газа в двух измерениях. Пусть имеется полоска полупроводникового материала макроскопических размеров в x и y направлениях, в то время как толщина полоски очень мала (нанометры). Периодические граничные условия в x и y направлениях приводит к следующим соотношениям для возможных значений волнового вектора:
Площадь, приходящаяся на одно значение вектора k в этом случае равняется
Число состояний внутри круга с радиусом k:
где учитывается двойное вырождение плотности состояний по спину. Число состояний, лежащих между значением волнового вектора k и k + dk, равняется
Аналогично, число состояний между энергиями E и E + dE можно рассчитать из следующего соотношения:
В результате, число состояний на единицу площади и единицу энергии, равняется:
Рассматривая электроны как свободные частицы, имеем соотношение:
соответственно, 2D -плотность электронных состояний принимает форму:
рис.2. Квантование энергий электрона в 2D-кристалле. Из (41) видно, что 2D-плотность состояний не зависит от энергии. Однако, ρ;(E) зависит от собственно энергетических состояний (уровней) и, т.о., представляет собой сумму от всех вкладов дискретных уровней:
где
ступенчатая функция Хевисайда и Ecn – отмечает минимумы зоны проводимости двумерного кристалла (рис.2). Дискретность уровней зоны проводимости следует из-за малости ширины двумерного кристалла. Фактически это один атом, уровни энергии которого обладают дискретным энергетическим спектром.
рис.3. Ступенчатая плотность электронных энергетических состояний в 2D-кристалле. Примером реализации 2D-кристаллов с запрещенным распространением электрона в одном направлении и разрешенным в двух других направлениях является GaAs – AlxGa1-xAs сверхрешетка, показанная на рис.4.
рис.4. Координатная потенциальная диаграмма сверхрешетки GaAs – AlxGa1-xAs.
|

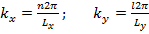 , n, l =1, 2,3…. (34)
, n, l =1, 2,3…. (34)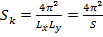 . (35)
. (35) , (36)
, (36)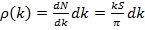 . (37)
. (37) . (38)
. (38) . (39)
. (39)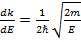 , (40)
, (40) . (41)
. (41)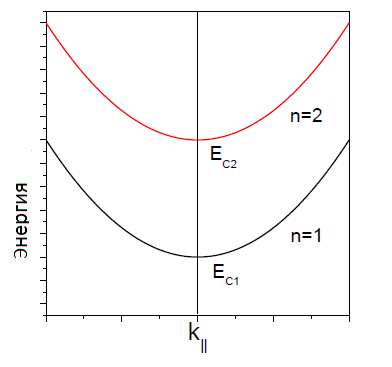
 , (42)
, (42)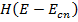 - (43)
- (43)




