Комментарий. Нахождение псевдорешений обычно  сложная задача, эквивалентная задаче выпуклого программирования (отыскание экстремумов многомерных, многопараметрических функций при некоторых ограничениях).
сложная задача, эквивалентная задаче выпуклого программирования (отыскание экстремумов многомерных, многопараметрических функций при некоторых ограничениях).
Определение. Псевдорешением (квазирешением) задачи 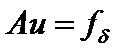 , где
, где 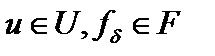 , а
, а 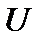 и
и 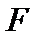 - банаховы пространства, называется любое решение
- банаховы пространства, называется любое решение  , минимизирующее невязку
, минимизирующее невязку  на компакте
на компакте 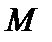 , где
, где  Таким образом,
Таким образом, 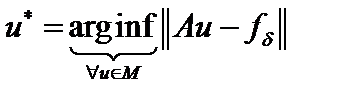 . Тогда
. Тогда 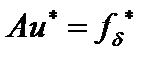 , где
, где  .
.
Ясно, что если проекция одна, то решение единственное. Если проекция не одна, то под псевдорешением понимается любой элемент из множества псевдорешений.
Теорема 3. Проекция 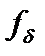 на множество
на множество  будет единственной, если множество
будет единственной, если множество 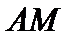 выпуклое. (Например,
выпуклое. (Например, 
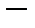 любое гильбертово пространство).
любое гильбертово пространство).

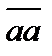 . Пусть имеется две проекции
. Пусть имеется две проекции  , то есть
, то есть 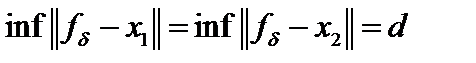 . По определению выпуклого множества
. По определению выпуклого множества 

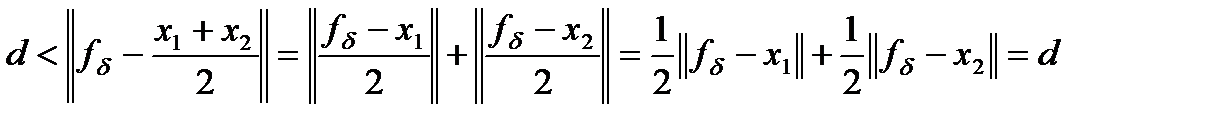 . Пусть
. Пусть  ,
, 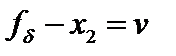 , тогда можно записать равенство параллелограмма:
, тогда можно записать равенство параллелограмма:


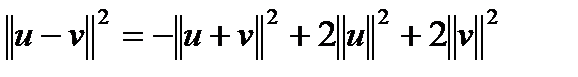
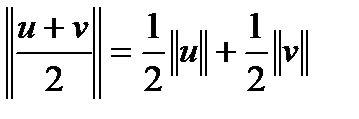 . Так как
. Так как  , то есть
, то есть 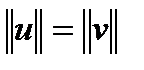 , то
, то
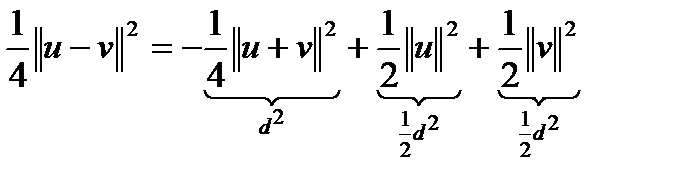

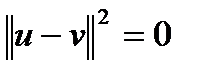

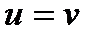

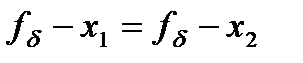

 .
. 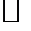
Теорема 4. Пусть однородное уравнение 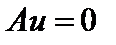 имеет только нулевое решение, множество
имеет только нулевое решение, множество 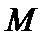 выпукло, а всякая сфера в пространстве
выпукло, а всякая сфера в пространстве  строго выпукла. Тогда квазирешение уравнения
строго выпукла. Тогда квазирешение уравнения  на компакте
на компакте 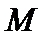 единственно и непрерывно зависит от правой части и.
единственно и непрерывно зависит от правой части и.
 Пусть
Пусть 
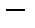 квазирешение и
квазирешение и  . Так как множество
. Так как множество  выпукло, то в силу линейности оператора
выпукло, то в силу линейности оператора 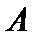 множество
множество  также выпукло. Очевидно, что
также выпукло. Очевидно, что  есть проекция элемента
есть проекция элемента  на множество
на множество 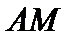 . В силу того, что сфера в пространстве
. В силу того, что сфера в пространстве 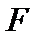 по условию теоремы строго выпукла, проекция
по условию теоремы строго выпукла, проекция 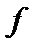 определяется однозначно. Далее доказательство завершается, как в теореме 3.
определяется однозначно. Далее доказательство завершается, как в теореме 3. 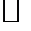
Рассмотрим применение проекционных методов для алгебраизированной задачи, то есть для СЛАУ.

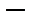 сложная задача, эквивалентная задаче выпуклого программирования (отыскание экстремумов многомерных, многопараметрических функций при некоторых ограничениях).
сложная задача, эквивалентная задаче выпуклого программирования (отыскание экстремумов многомерных, многопараметрических функций при некоторых ограничениях).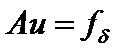 , где
, где 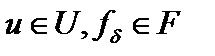 , а
, а 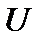 и
и 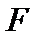 - банаховы пространства, называется любое решение
- банаховы пространства, называется любое решение  , минимизирующее невязку
, минимизирующее невязку  на компакте
на компакте 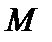 , где
, где  Таким образом,
Таким образом, 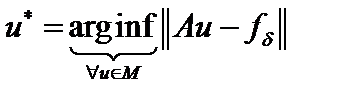 . Тогда
. Тогда 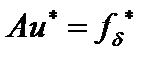 , где
, где  .
.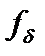 на множество
на множество  будет единственной, если множество
будет единственной, если множество 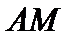 выпуклое. (Например,
выпуклое. (Например, 
 любое гильбертово пространство).
любое гильбертово пространство).
 . Пусть имеется две проекции
. Пусть имеется две проекции  , то есть
, то есть 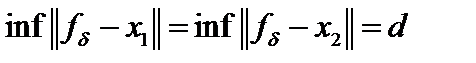 . По определению выпуклого множества
. По определению выпуклого множества 

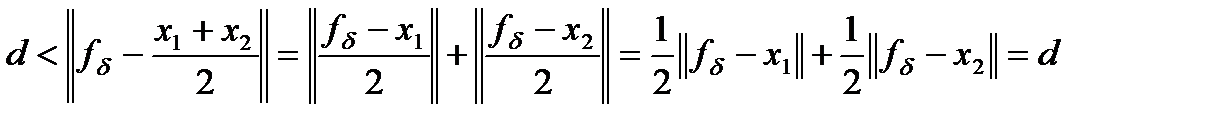 . Пусть
. Пусть  ,
, 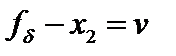 , тогда можно записать равенство параллелограмма:
, тогда можно записать равенство параллелограмма:

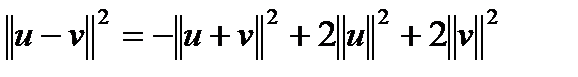
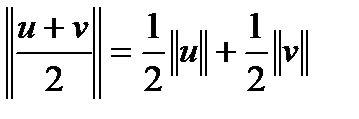 . Так как
. Так как  , то есть
, то есть 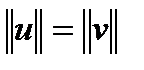 , то
, то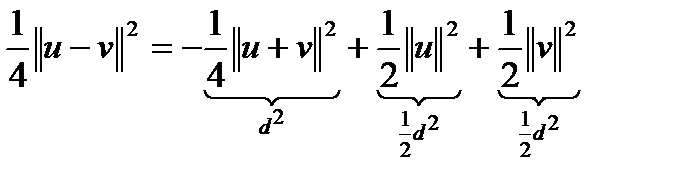
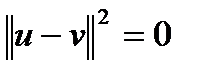
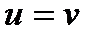
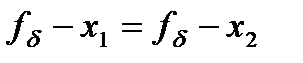
 .
. 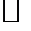
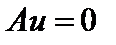 имеет только нулевое решение, множество
имеет только нулевое решение, множество 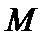 выпукло, а всякая сфера в пространстве
выпукло, а всякая сфера в пространстве  строго выпукла. Тогда квазирешение уравнения
строго выпукла. Тогда квазирешение уравнения  на компакте
на компакте 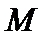 единственно и непрерывно зависит от правой части и.
единственно и непрерывно зависит от правой части и.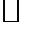 Пусть
Пусть 
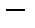 квазирешение и
квазирешение и  . Так как множество
. Так как множество  выпукло, то в силу линейности оператора
выпукло, то в силу линейности оператора 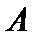 множество
множество  также выпукло. Очевидно, что
также выпукло. Очевидно, что  есть проекция элемента
есть проекция элемента  на множество
на множество 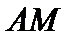 . В силу того, что сфера в пространстве
. В силу того, что сфера в пространстве 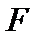 по условию теоремы строго выпукла, проекция
по условию теоремы строго выпукла, проекция 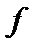 определяется однозначно. Далее доказательство завершается, как в теореме 3.
определяется однозначно. Далее доказательство завершается, как в теореме 3.