Пусть рассматривается система уравнений  , тогда
, тогда  - невязка.
- невязка.
Комментарий. 1. Нелинейный оператор  непрерывен в точке
непрерывен в точке  , если
, если 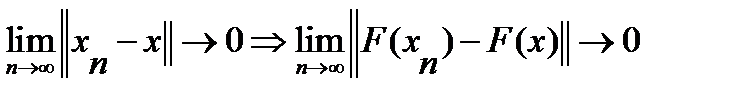 ; вполне непрерывен, если он непрерывен
; вполне непрерывен, если он непрерывен 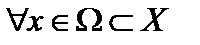 и ограниченные множества отображает в предкомпактные. В отличие от линейного случая непрерывность в точке не гарантирует непрерывности во всём пространстве и не связана с ограниченностью.
и ограниченные множества отображает в предкомпактные. В отличие от линейного случая непрерывность в точке не гарантирует непрерывности во всём пространстве и не связана с ограниченностью.
Нелинейный оператор 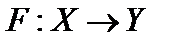 дифференцируем по Фреше в точке
дифференцируем по Фреше в точке  , если существует линейный ограниченный оператор
, если существует линейный ограниченный оператор 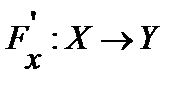 (производная Фреше в точке
(производная Фреше в точке 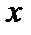 или сильная производная), такой, что
или сильная производная), такой, что 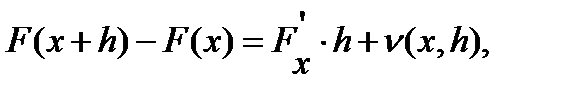 причём
причём 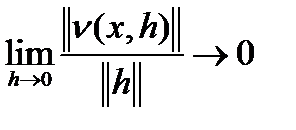 . Линейная часть приращения
. Линейная часть приращения 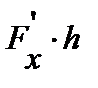
 дифференциал Фреше.
дифференциал Фреше.
Производная Фреше нелинейного оператора  - это оператор
- это оператор  , действующий как функция от х. В частном случае нелинейного функционала
, действующий как функция от х. В частном случае нелинейного функционала  совокупность всех таких функционалов, определённых на X, образует сопряжённое пространство E*, поэтому производная Фреше
совокупность всех таких функционалов, определённых на X, образует сопряжённое пространство E*, поэтому производная Фреше  функционала
функционала 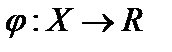
 это вектор из E*:
это вектор из E*: 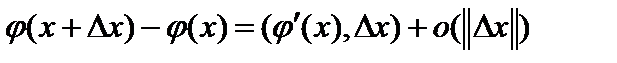 . Его называют градиентом Фреше:
. Его называют градиентом Фреше: 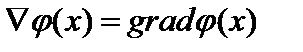 .
.
Дифференциал Гато (слабый дифференциал)  это предел по норме
это предел по норме 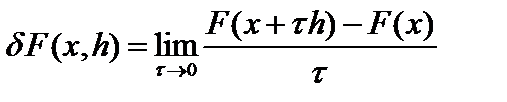 . Если этот предел линеен по
. Если этот предел линеен по 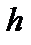 , то есть
, то есть 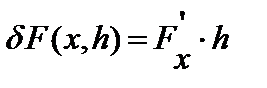 , то оператор
, то оператор 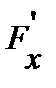 называется производной Гато в точке
называется производной Гато в точке  .
.
Производная Фреше в точке 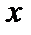 совпадает с производной Гато в точке
совпадает с производной Гато в точке 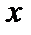 . Производная Гато в точке
. Производная Гато в точке 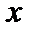 совпадает с производной Фреше в точке
совпадает с производной Фреше в точке  , если производная Гато непрерывна по
, если производная Гато непрерывна по 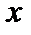 в этой точке.
в этой точке.
2. Дифференцируемость всегда сводится к возможности линейной аппроксимации  . В одномерном случае
. В одномерном случае 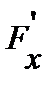
 обычная производная, в случае
обычная производная, в случае  переменных
переменных 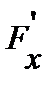
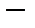 градиент, а
градиент, а 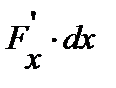 - скалярное произведение, для оператора
- скалярное произведение, для оператора 

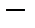 матрица Якоби
матрица Якоби 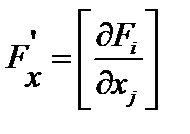 , а
, а 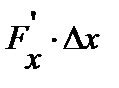 есть умножение матрицы на вектор. Скалярное произведение можно представить как функционал (функцию
есть умножение матрицы на вектор. Скалярное произведение можно представить как функционал (функцию 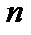 переменных в конечномерном случае) и тогда дифференциал от неё
переменных в конечномерном случае) и тогда дифференциал от неё 
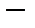 тоже скалярное произведение. Например, в случае двумерного пространства
тоже скалярное произведение. Например, в случае двумерного пространства 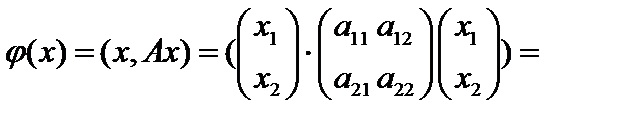
 . Тогда полный дифференциал
. Тогда полный дифференциал  . После несложных преобразований получим
. После несложных преобразований получим  . Дифференциал Фреше можно найти и сразу, как дифференциал от скалярного произведения:
. Дифференциал Фреше можно найти и сразу, как дифференциал от скалярного произведения: 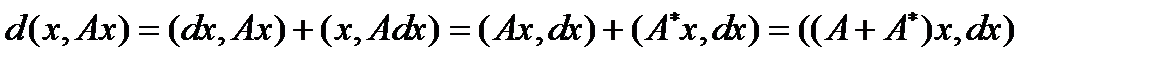 .
.
Введем понятие нормальной системы. Пусть 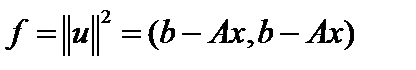 . Тогда, приравнивая дифференциал Фреше к нулю, получим
. Тогда, приравнивая дифференциал Фреше к нулю, получим
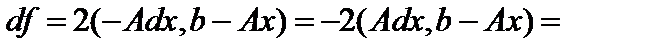
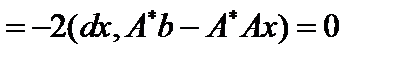 . Тогда исходная система равносильна системе уравнений
. Тогда исходная система равносильна системе уравнений 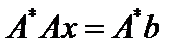 .
.

 , тогда
, тогда  - невязка.
- невязка. непрерывен в точке
непрерывен в точке  , если
, если 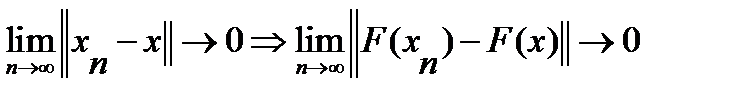 ; вполне непрерывен, если он непрерывен
; вполне непрерывен, если он непрерывен 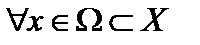 и ограниченные множества отображает в предкомпактные. В отличие от линейного случая непрерывность в точке не гарантирует непрерывности во всём пространстве и не связана с ограниченностью.
и ограниченные множества отображает в предкомпактные. В отличие от линейного случая непрерывность в точке не гарантирует непрерывности во всём пространстве и не связана с ограниченностью.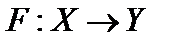 дифференцируем по Фреше в точке
дифференцируем по Фреше в точке  , если существует линейный ограниченный оператор
, если существует линейный ограниченный оператор 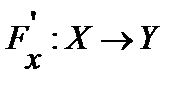 (производная Фреше в точке
(производная Фреше в точке 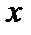 или сильная производная), такой, что
или сильная производная), такой, что 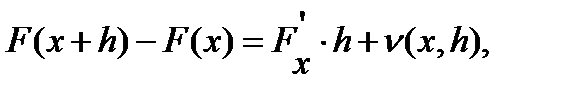 причём
причём 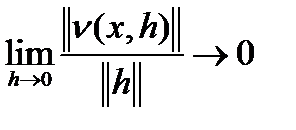 . Линейная часть приращения
. Линейная часть приращения 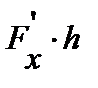
 дифференциал Фреше.
дифференциал Фреше. - это оператор
- это оператор  , действующий как функция от х. В частном случае нелинейного функционала
, действующий как функция от х. В частном случае нелинейного функционала  совокупность всех таких функционалов, определённых на X, образует сопряжённое пространство E*, поэтому производная Фреше
совокупность всех таких функционалов, определённых на X, образует сопряжённое пространство E*, поэтому производная Фреше  функционала
функционала 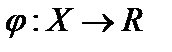
 это вектор из E*:
это вектор из E*: 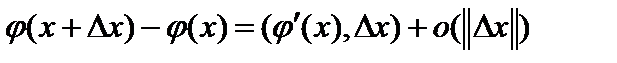 . Его называют градиентом Фреше:
. Его называют градиентом Фреше: 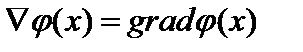 .
. это предел по норме
это предел по норме 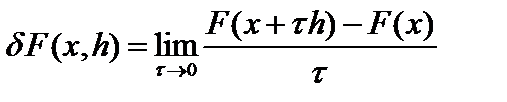 . Если этот предел линеен по
. Если этот предел линеен по 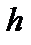 , то есть
, то есть 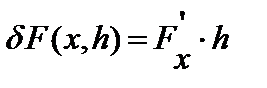 , то оператор
, то оператор 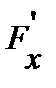 называется производной Гато в точке
называется производной Гато в точке  .
.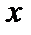 совпадает с производной Гато в точке
совпадает с производной Гато в точке 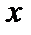 . Производная Гато в точке
. Производная Гато в точке 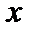 совпадает с производной Фреше в точке
совпадает с производной Фреше в точке  , если производная Гато непрерывна по
, если производная Гато непрерывна по 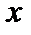 в этой точке.
в этой точке. . В одномерном случае
. В одномерном случае 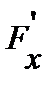
 обычная производная, в случае
обычная производная, в случае  переменных
переменных 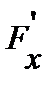
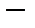 градиент, а
градиент, а 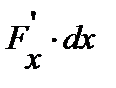 - скалярное произведение, для оператора
- скалярное произведение, для оператора 

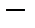 матрица Якоби
матрица Якоби 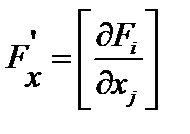 , а
, а 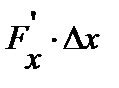 есть умножение матрицы на вектор. Скалярное произведение можно представить как функционал (функцию
есть умножение матрицы на вектор. Скалярное произведение можно представить как функционал (функцию 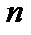 переменных в конечномерном случае) и тогда дифференциал от неё
переменных в конечномерном случае) и тогда дифференциал от неё 
 тоже скалярное произведение. Например, в случае двумерного пространства
тоже скалярное произведение. Например, в случае двумерного пространства 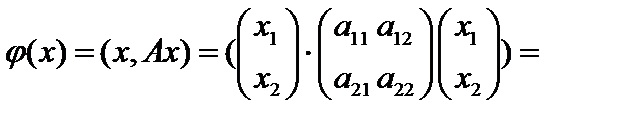
 . Тогда полный дифференциал
. Тогда полный дифференциал  . После несложных преобразований получим
. После несложных преобразований получим  . Дифференциал Фреше можно найти и сразу, как дифференциал от скалярного произведения:
. Дифференциал Фреше можно найти и сразу, как дифференциал от скалярного произведения: 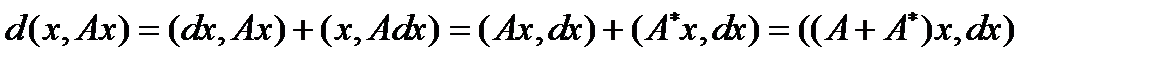 .
.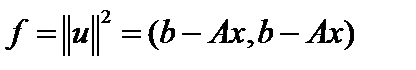 . Тогда, приравнивая дифференциал Фреше к нулю, получим
. Тогда, приравнивая дифференциал Фреше к нулю, получим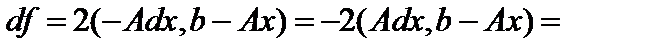
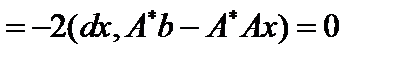 . Тогда исходная система равносильна системе уравнений
. Тогда исходная система равносильна системе уравнений 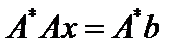 .
.


