VII. ПРОЕКЦИОННЫЕ МЕТОДЫ. ПСЕВДОРЕШЕНИЕ
- Г-голубчики, сказал Федор Симеонович озадаченно... Это же проблема Бен Б-бецалеля. К-калиостро же доказал, что она н-не имеет р-решения.
- Мы сами знаем, что она не имеет решения, сказал Хунта, немедленно ощетиниваясь. – Мы хотим знать, как ее решать.
- К-как-то ты странно рассуждаешь, К-кристо... К-как же искать решение, к-когда его нет? Б-бессмыслица какая-то...
- Извини, Теодор, но это ты очень странно рассуждаешь. Бессмыслица - искать решение, если оно и так есть. Речь идет о том, как поступать с задачей, которая решения не имеет. Это глубоко принципиальный вопрос...
А. Стругацкий, Б. Стругацкий.
Понедельник начинается в субботу
Проблема Бецалеля. Постановка задачи
Пусть 
 банахово пространство, а
банахово пространство, а 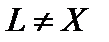
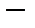 конечномерное подпространство, не совпадающее с
конечномерное подпространство, не совпадающее с  .При использовании проекционных методов исходная постановка задачи, как правило, является компромиссом между, быть может, противоречивыми требованиями. Такие задачи или принципиально не имеют решения, или решение не единственно. И то и другое может сопровождаться операторной неустойчивостью.
.При использовании проекционных методов исходная постановка задачи, как правило, является компромиссом между, быть может, противоречивыми требованиями. Такие задачи или принципиально не имеют решения, или решение не единственно. И то и другое может сопровождаться операторной неустойчивостью.
Определение. Задачей Чебышева называют любую задачу о наилучшем приближении элемента  банахова пространства
банахова пространства 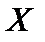 к конечномерному подпространству
к конечномерному подпространству 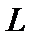 . Она ставится так:
. Она ставится так:  , надо указать элемент
, надо указать элемент 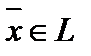 , такой, что
, такой, что 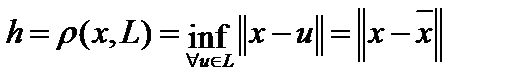 .
.
Комментарий. Ясно, что элемент  будет приближать любой элемент
будет приближать любой элемент  лучше, чем другие элементы из
лучше, чем другие элементы из  . Не ясно, существует ли такой элемент и единственен ли он.
. Не ясно, существует ли такой элемент и единственен ли он.

Теорема 1 (существование наилучшего приближения). Наилучшее приближение элемента  банахова пространства
банахова пространства  к конечномерному подпространству
к конечномерному подпространству  существует.
существует.
 Пусть
Пусть 
 банахово пространство, а
банахово пространство, а 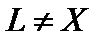
 конечномерное подпространство, не совпадающее с
конечномерное подпространство, не совпадающее с  . Укажем элемент
. Укажем элемент  , такой, что
, такой, что 
 . Для этого введём в
. Для этого введём в  некоторый базис
некоторый базис 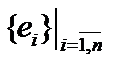 . Тогда
. Тогда  . Соответствующая эвклидова норма в эвклидовом базисе
. Соответствующая эвклидова норма в эвклидовом базисе 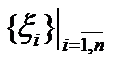 имеет вид
имеет вид  . В конечномерных пространствах все нормы эквивалентны, то есть
. В конечномерных пространствах все нормы эквивалентны, то есть  . Рассмотрим функцию
. Рассмотрим функцию  ,
,  . Она непрерывна, так как
. Она непрерывна, так как 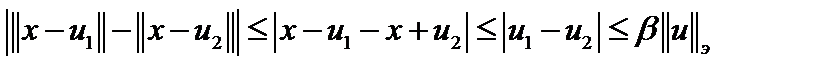 , то есть если, то и
, то есть если, то и  . Рассмотрим теперь шар
. Рассмотрим теперь шар  , где
, где 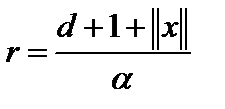 . Вне шара
. Вне шара  . Так как
. Так как 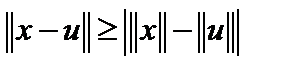 , и так как
, и так как 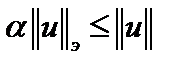 , а
, а  , то
, то  и неравенство только усилится, если
и неравенство только усилится, если  заменить на меньшее выражение
заменить на меньшее выражение 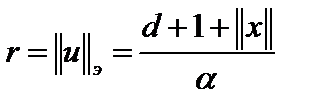 . Тогда
. Тогда 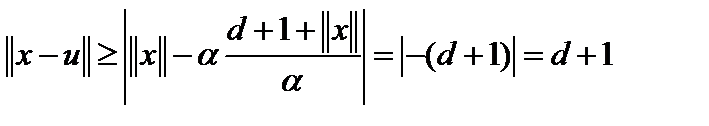 . Таким образом, инфинум
. Таким образом, инфинум 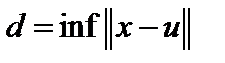 недостижим вне этого шара. Это означает, что внутри шара, то есть замкнутого ограниченного множества в конечномерном пространстве, то есть компакта, функция
недостижим вне этого шара. Это означает, что внутри шара, то есть замкнутого ограниченного множества в конечномерном пространстве, то есть компакта, функция 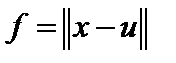 достигает инфинума (теорема Вейерштрасса).
достигает инфинума (теорема Вейерштрасса). 
Комментарий. Таким образом, наилучшее приближение элемента х пространства  к подпространству L существует. Покажем, что оно не единственно. Пусть пространство Х есть плоскость
к подпространству L существует. Покажем, что оно не единственно. Пусть пространство Х есть плоскость 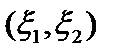 , а
, а 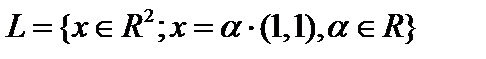 . Введём на Х норму
. Введём на Х норму  . Пусть
. Пусть  .
.

Тогда  .
.

Из графика этой функции видно, что при  решение не единственно.
решение не единственно.
Определение. Множество 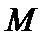 называется выпуклым, если из того, что
называется выпуклым, если из того, что 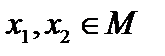 , следует, что
, следует, что 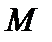 принадлежит и весь отрезок, соединяющий точки
принадлежит и весь отрезок, соединяющий точки  , то есть совокупность всех точек х вида
, то есть совокупность всех точек х вида 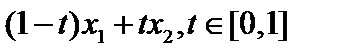 .
.
Определение. Банахово пространство  называется строго выпуклым, если
называется строго выпуклым, если  для любого действительного скаляра
для любого действительного скаляра  и любых
и любых  .
.
Комментарий. Пространства 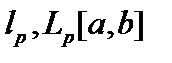 при
при 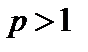 строго выпуклы, а при
строго выпуклы, а при 
 нет. Пространство
нет. Пространство  не строго выпукло. Показано, что в нём проекция единственна только на подмножестве полиномов степени не выше
не строго выпукло. Показано, что в нём проекция единственна только на подмножестве полиномов степени не выше 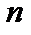 .
.
Теорема 2 (единственность наилучшего приближения).
Пусть 
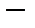 строго выпуклое банахово пространство, а
строго выпуклое банахово пространство, а 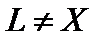
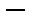 конечномерное подпространство, не совпадающее с Х, причём
конечномерное подпространство, не совпадающее с Х, причём  . Тогда
. Тогда 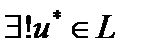 , такой, что
, такой, что 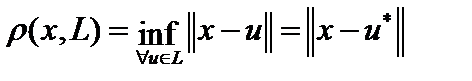 .
.
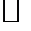 Существование доказано в теореме 1. Осталось показатьединственность.
Существование доказано в теореме 1. Осталось показатьединственность.
 . Пусть
. Пусть 
 два наилучших приближения какого-то х. Тогда
два наилучших приближения какого-то х. Тогда  .
.
Так как 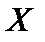
 строго выпуклое банахово пространство, то
строго выпуклое банахово пространство, то  , так как при
, так как при 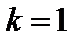
 . Тогда
. Тогда  , так как это линейная комбинация элементов из
, так как это линейная комбинация элементов из 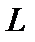 . Но по условию
. Но по условию 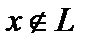 . Это противоречие и доказывает теорему.
. Это противоречие и доказывает теорему. 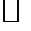
Комментарий. 1. Как найти наилучшее приближение? В банаховых пространствах общего способа не существует. В гильбертовых пространствах такой общий способ даёт задача ортогонализации, приводящая к понятию ряда Фурье. Пусть  – подпространство гильбертова пространства, а
– подпространство гильбертова пространства, а 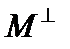
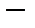 подпространство, ортогональное к
подпространство, ортогональное к  . Тогда гильбертово пространство
. Тогда гильбертово пространство 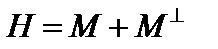 . Так как
. Так как  – сепарабельное пространство, то в нем всегда есть ортонормированная система векторов:
– сепарабельное пространство, то в нем всегда есть ортонормированная система векторов:  , где
, где 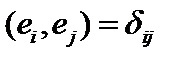
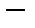 символ Кронекера. Проекция вектора
символ Кронекера. Проекция вектора  на
на 
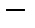 вектор
вектор  , где
, где  . Мы будем искать те значения коэффициентов разложения
. Мы будем искать те значения коэффициентов разложения  , при которых невязка (квадрат невязки)
, при которых невязка (квадрат невязки)  будет минимальна:
будет минимальна:
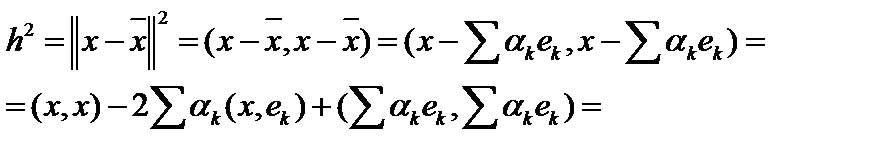
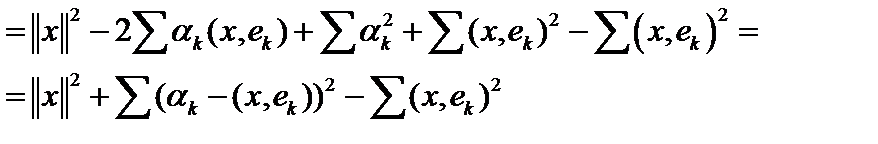 .
.
Ясно, что это выражение будет принимать минимальное значение при 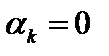 и
и  . Тогда
. Тогда 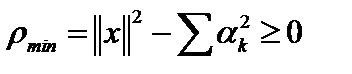 . Отсюда получаем неравенство Бесселя
. Отсюда получаем неравенство Бесселя  . При
. При 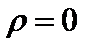 ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова –Парсеваля
ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова –Парсеваля 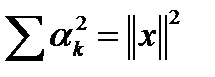
 теорему Пифагора для гильбертовых пространств.
теорему Пифагора для гильбертовых пространств.
2. Пусть  , где
, где 
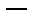 компактный оператор. Если
компактный оператор. Если  , где
, где 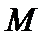
 компакт, то в соответствии с теоремой Тихонова такая задача условно устойчива. Рассмотрим случай, когда
компакт, то в соответствии с теоремой Тихонова такая задача условно устойчива. Рассмотрим случай, когда  .
.
Задача Чебышёва в применении к решению операторных уравнений I рода приводит к понятию псевдорешения (квазирешения) и методу В.К.Иванова нахождения псевдорешений.


 банахово пространство, а
банахово пространство, а 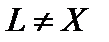
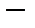 конечномерное подпространство, не совпадающее с
конечномерное подпространство, не совпадающее с  .При использовании проекционных методов исходная постановка задачи, как правило, является компромиссом между, быть может, противоречивыми требованиями. Такие задачи или принципиально не имеют решения, или решение не единственно. И то и другое может сопровождаться операторной неустойчивостью.
.При использовании проекционных методов исходная постановка задачи, как правило, является компромиссом между, быть может, противоречивыми требованиями. Такие задачи или принципиально не имеют решения, или решение не единственно. И то и другое может сопровождаться операторной неустойчивостью. банахова пространства
банахова пространства 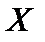 к конечномерному подпространству
к конечномерному подпространству 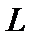 . Она ставится так:
. Она ставится так:  , надо указать элемент
, надо указать элемент 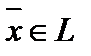 , такой, что
, такой, что 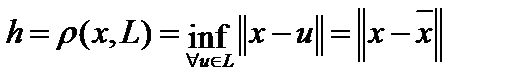 .
. будет приближать любой элемент
будет приближать любой элемент  лучше, чем другие элементы из
лучше, чем другие элементы из  . Не ясно, существует ли такой элемент и единственен ли он.
. Не ясно, существует ли такой элемент и единственен ли он. банахова пространства
банахова пространства  к конечномерному подпространству
к конечномерному подпространству  существует.
существует.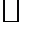 Пусть
Пусть 
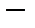 банахово пространство, а
банахово пространство, а 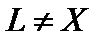
 конечномерное подпространство, не совпадающее с
конечномерное подпространство, не совпадающее с  . Укажем элемент
. Укажем элемент  , такой, что
, такой, что 
 . Для этого введём в
. Для этого введём в  некоторый базис
некоторый базис 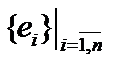 . Тогда
. Тогда  . Соответствующая эвклидова норма в эвклидовом базисе
. Соответствующая эвклидова норма в эвклидовом базисе 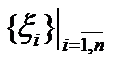 имеет вид
имеет вид  . В конечномерных пространствах все нормы эквивалентны, то есть
. В конечномерных пространствах все нормы эквивалентны, то есть  . Рассмотрим функцию
. Рассмотрим функцию  ,
,  . Она непрерывна, так как
. Она непрерывна, так как 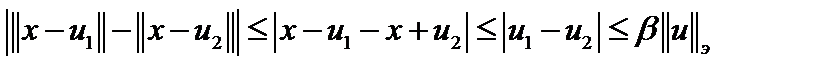 , то есть если, то и
, то есть если, то и  . Рассмотрим теперь шар
. Рассмотрим теперь шар  , где
, где 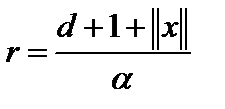 . Вне шара
. Вне шара  . Так как
. Так как 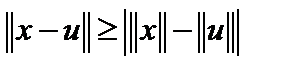 , и так как
, и так как 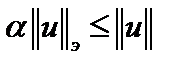 , а
, а  , то
, то  и неравенство только усилится, если
и неравенство только усилится, если  заменить на меньшее выражение
заменить на меньшее выражение 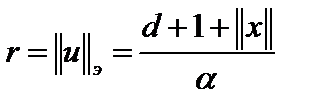 . Тогда
. Тогда 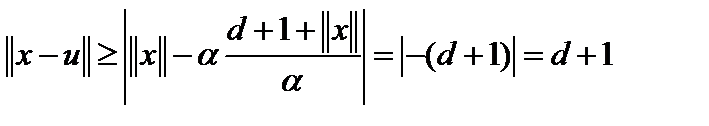 . Таким образом, инфинум
. Таким образом, инфинум 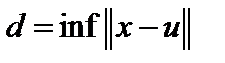 недостижим вне этого шара. Это означает, что внутри шара, то есть замкнутого ограниченного множества в конечномерном пространстве, то есть компакта, функция
недостижим вне этого шара. Это означает, что внутри шара, то есть замкнутого ограниченного множества в конечномерном пространстве, то есть компакта, функция 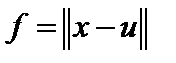 достигает инфинума (теорема Вейерштрасса).
достигает инфинума (теорема Вейерштрасса). 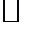
 к подпространству L существует. Покажем, что оно не единственно. Пусть пространство Х есть плоскость
к подпространству L существует. Покажем, что оно не единственно. Пусть пространство Х есть плоскость 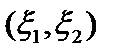 , а
, а 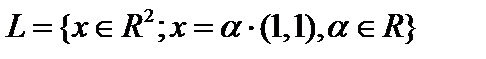 . Введём на Х норму
. Введём на Х норму  . Пусть
. Пусть  .
. .
. решение не единственно.
решение не единственно.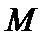 называется выпуклым, если из того, что
называется выпуклым, если из того, что 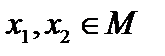 , следует, что
, следует, что 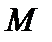 принадлежит и весь отрезок, соединяющий точки
принадлежит и весь отрезок, соединяющий точки  , то есть совокупность всех точек х вида
, то есть совокупность всех точек х вида 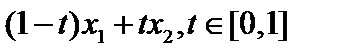 .
. называется строго выпуклым, если
называется строго выпуклым, если  для любого действительного скаляра
для любого действительного скаляра  и любых
и любых  .
.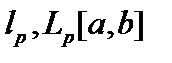 при
при 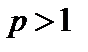 строго выпуклы, а при
строго выпуклы, а при 
 нет. Пространство
нет. Пространство  не строго выпукло. Показано, что в нём проекция единственна только на подмножестве полиномов степени не выше
не строго выпукло. Показано, что в нём проекция единственна только на подмножестве полиномов степени не выше 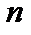 .
.
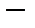 строго выпуклое банахово пространство, а
строго выпуклое банахово пространство, а 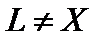
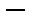 конечномерное подпространство, не совпадающее с Х, причём
конечномерное подпространство, не совпадающее с Х, причём  . Тогда
. Тогда 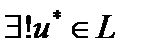 , такой, что
, такой, что 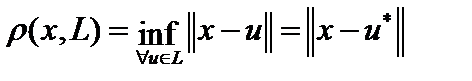 .
.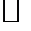 Существование доказано в теореме 1. Осталось показатьединственность.
Существование доказано в теореме 1. Осталось показатьединственность. . Пусть
. Пусть 
 два наилучших приближения какого-то х. Тогда
два наилучших приближения какого-то х. Тогда  .
.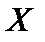
 строго выпуклое банахово пространство, то
строго выпуклое банахово пространство, то  , так как при
, так как при 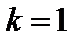
 . Тогда
. Тогда  , так как это линейная комбинация элементов из
, так как это линейная комбинация элементов из 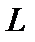 . Но по условию
. Но по условию 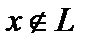 . Это противоречие и доказывает теорему.
. Это противоречие и доказывает теорему. 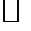
 – подпространство гильбертова пространства, а
– подпространство гильбертова пространства, а 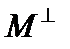
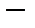 подпространство, ортогональное к
подпространство, ортогональное к  . Тогда гильбертово пространство
. Тогда гильбертово пространство 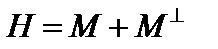 . Так как
. Так как  – сепарабельное пространство, то в нем всегда есть ортонормированная система векторов:
– сепарабельное пространство, то в нем всегда есть ортонормированная система векторов:  , где
, где 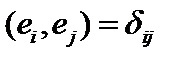
 символ Кронекера. Проекция вектора
символ Кронекера. Проекция вектора  на
на 
 вектор
вектор  , где
, где  . Мы будем искать те значения коэффициентов разложения
. Мы будем искать те значения коэффициентов разложения  , при которых невязка (квадрат невязки)
, при которых невязка (квадрат невязки)  будет минимальна:
будет минимальна: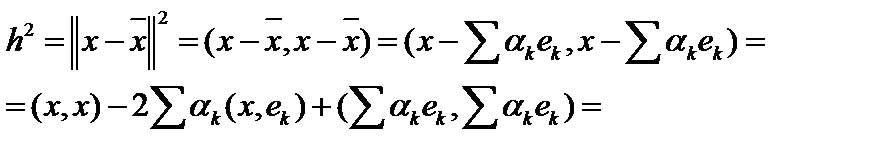
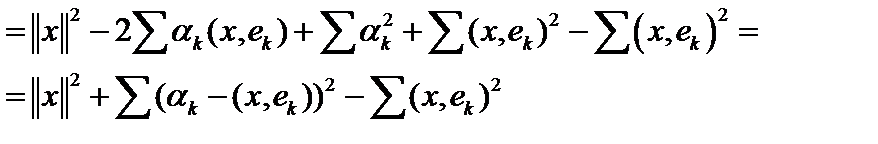 .
.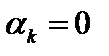 и
и  . Тогда
. Тогда 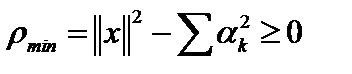 . Отсюда получаем неравенство Бесселя
. Отсюда получаем неравенство Бесселя  . При
. При 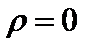 ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова –Парсеваля
ортонормированная система векторов (ОНС) называется полной ортонормированной системой в смысле Стеклова (ПОНС). Отсюда можно получить равенство Стеклова –Парсеваля 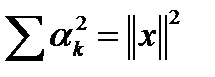
 теорему Пифагора для гильбертовых пространств.
теорему Пифагора для гильбертовых пространств. , где
, где 
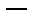 компактный оператор. Если
компактный оператор. Если  , где
, где 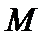
 компакт, то в соответствии с теоремой Тихонова такая задача условно устойчива. Рассмотрим случай, когда
компакт, то в соответствии с теоремой Тихонова такая задача условно устойчива. Рассмотрим случай, когда  .
.


