Комментарий. Восстанавливая траектории комет по наблюдениям, Лежандр (1806 г.) и Гаусс (1809 г.) поставили и решили задачу нахождения значений параметров  , связывающих набор экспериментальных данных
, связывающих набор экспериментальных данных  , полученных с неизбежными систематическими и случайными ошибками. Естественно, надо провести как можно большее число
, полученных с неизбежными систематическими и случайными ошибками. Естественно, надо провести как можно большее число 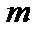 измерений, то есть
измерений, то есть 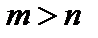 , где
, где 
 число независимых параметров. Функция, связывающая экспериментальные данные
число независимых параметров. Функция, связывающая экспериментальные данные 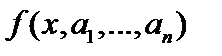 , известна априори, как и результаты измерений
, известна априори, как и результаты измерений  и
и  . Причём каждое измерение давало линейное соотношение между ними вида
. Причём каждое измерение давало линейное соотношение между ними вида  . Необходимо найти значения параметров
. Необходимо найти значения параметров  . Это типичная некорректная задача. Идея её решения состояла в том, чтобы определить решениекак такое, которое минимизирует сумму квадратов отклонений всех измерений, то есть квадратичный функционал невязки
. Это типичная некорректная задача. Идея её решения состояла в том, чтобы определить решениекак такое, которое минимизирует сумму квадратов отклонений всех измерений, то есть квадратичный функционал невязки  . Тогда
. Тогда  .
.
| хi
|
|
|
|
|
|
| уi
| 6,1
| 7,1
| 6,6
| 4,6
| 5,1
|
Пример. Пусть проведено 5 измерений и зависимость между ними 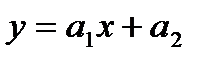 задана таблицей.
задана таблицей.
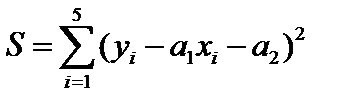 ,
, 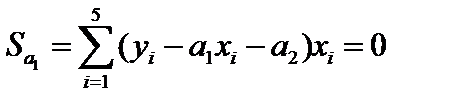 ,
, 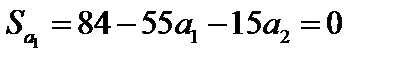 ,
, 
 .
.
Тогда уравнение прямой имеет вид 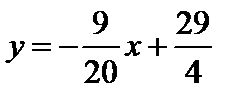 .
.
Если связать эту задачу с предыдущим примером, то мы получим линейную оболочку  и задача ставится так: найти проекцию вектора
и задача ставится так: найти проекцию вектора 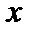 на линейную оболочку
на линейную оболочку 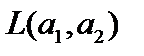 то есть псевдорешение.
то есть псевдорешение. 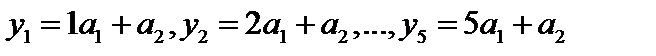 ,
, 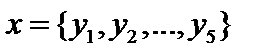 = {6,1; 7,1; 6,6; 4,6; 5,1} a1 = {1,2,3,4,5}, a2 = {1,1,1,1,1}.
= {6,1; 7,1; 6,6; 4,6; 5,1} a1 = {1,2,3,4,5}, a2 = {1,1,1,1,1}.
Пусть теперь 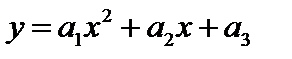 . Тогда
. Тогда 
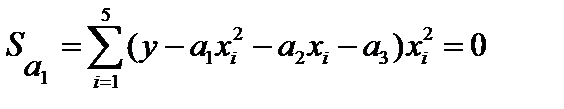


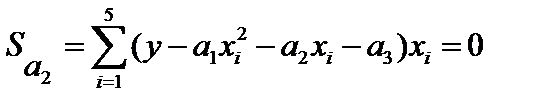



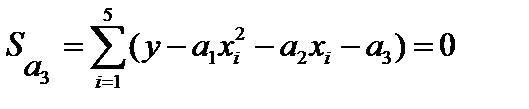
 . Этот метод называется методом наименьших квадратов или методом невязки.
. Этот метод называется методом наименьших квадратов или методом невязки.
Пример. Получить псевдорешение системы: 
Составим матрицу Грама. 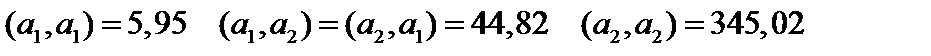 , где
, где  .
.
Тогда правая часть получившейся СЛАУ (31,91; 245,28), а решение имеет вид 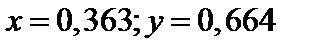 .
.

 , связывающих набор экспериментальных данных
, связывающих набор экспериментальных данных  , полученных с неизбежными систематическими и случайными ошибками. Естественно, надо провести как можно большее число
, полученных с неизбежными систематическими и случайными ошибками. Естественно, надо провести как можно большее число 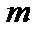 измерений, то есть
измерений, то есть 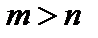 , где
, где 
 число независимых параметров. Функция, связывающая экспериментальные данные
число независимых параметров. Функция, связывающая экспериментальные данные 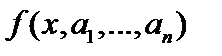 , известна априори, как и результаты измерений
, известна априори, как и результаты измерений  и
и  . Причём каждое измерение давало линейное соотношение между ними вида
. Причём каждое измерение давало линейное соотношение между ними вида  . Необходимо найти значения параметров
. Необходимо найти значения параметров  . Это типичная некорректная задача. Идея её решения состояла в том, чтобы определить решениекак такое, которое минимизирует сумму квадратов отклонений всех измерений, то есть квадратичный функционал невязки
. Это типичная некорректная задача. Идея её решения состояла в том, чтобы определить решениекак такое, которое минимизирует сумму квадратов отклонений всех измерений, то есть квадратичный функционал невязки  . Тогда
. Тогда  .
.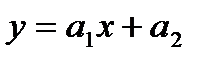 задана таблицей.
задана таблицей.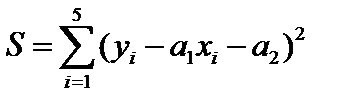 ,
, 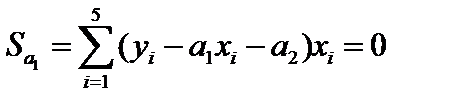 ,
, 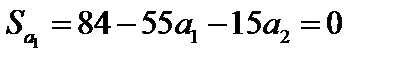 ,
, 
 .
.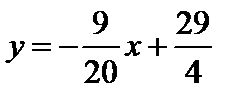 .
. и задача ставится так: найти проекцию вектора
и задача ставится так: найти проекцию вектора 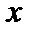 на линейную оболочку
на линейную оболочку 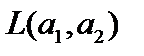 то есть псевдорешение.
то есть псевдорешение. 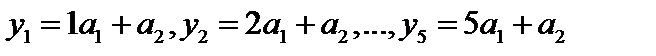 ,
, 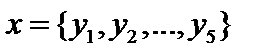 = {6,1; 7,1; 6,6; 4,6; 5,1} a1 = {1,2,3,4,5}, a2 = {1,1,1,1,1}.
= {6,1; 7,1; 6,6; 4,6; 5,1} a1 = {1,2,3,4,5}, a2 = {1,1,1,1,1}.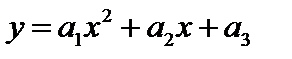 . Тогда
. Тогда 
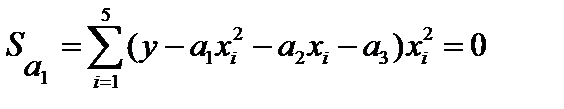


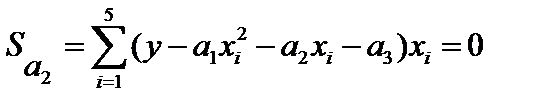



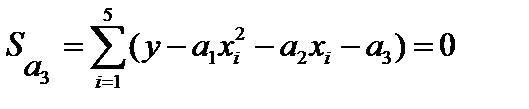
 . Этот метод называется методом наименьших квадратов или методом невязки.
. Этот метод называется методом наименьших квадратов или методом невязки.
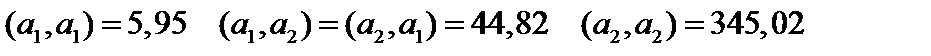 , где
, где  .
.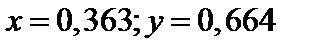 .
.


