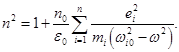Аномальная и нормальная дисперсия света. Связь дисперсии и поглощения
Задача Связать угол наименьшего отклонения луча в призме с преломляющим углом и показателем преломления призмы. Дано:
Найти:
Решение:
Обозначим за
Угол падения на внутреннюю поверхность
Закон преломления для внутренней поверхности
(1) откуда также можем получить
(2) Угол преломления
(3) Ввиду очевидной симметрии уравнений (1)-(2) относительно перестановки, легко заключить что минимум суммы, стоящей в скобках уравнения (3) выполняется при выполнении условия:
Подставим в уравнение (1):
Подставим в уравнение (3), чтобы получить выражение для угла наименьшего преломления:
Аномальная и нормальная дисперсия света. Связь дисперсии и поглощения Макроскопическая теория Максвелла не может объяснить дисперсию света. Из теории Максвелла следует, что Для воды ε = 81, следовательно, ε(ω) < ε(0), поэтому n(ω) < n(0). Т.е. для каждой частоты будет свой показатель преломления. Поэтому нужно учитывать зависимость n от частоты. Явление дисперсии можно объяснить, рассматривая взаимодействие световой волны с веществом. Такое стало возможным благодаря классической электронной теории Лоренца. Согласно классической электронной теории электроны в атоме совершают колебания под действием квазиупругой силы. Световая волн, падающая на диэлектрик, заставляет электроны, находящиеся в атоме этого диэлектрика, совершать вынужденные колебания, частота которых совпадает с частотой вынуждающей силы. Но электроны, движущиеся ускоренно излучают электромагнитные волны. Эти вторичны волны, излучаемые электронами атомов вещества, имеют ту же частоту, что и падающая волна. Начальные фазы могут различаться. Эти вторичные волны интерферируют с падающей волной, и в веществе распространяется результирующая волна, направление которой совпадает с направлением падающей волны, скорость которой зависит от частоты (а в вакууме равна скорости света). Следовательно, показатель преломления n зависит от частоты ω;.
где χ – диэлектрическая восприимчивость вещества, Р – вектор поляризации (результирующий дипольный момент единицы объёма). Согласно теории Максвелла
В условиях, когда на вещество падает световая волна, электрическое поле изменяется столь быстро, что поляризуемость (нас будет интересовать только электронная, т.е. индуцированная полем световой волны) не успевает изменяться за полем. В этом случае
где n0 – количество атомов в единице объёма, РЕ – индуцированный дипольный момент одного атома. Можно показать, что наиболее сильному воздействию электрического поля световой волны подвергаются наиболее слабо связанные с ядром электроны, так называемые оптические электроны. Для простоты считаем, что каждый атом содержит один оптический электрон. Тогда
х - смещение.
т.е. n зависит от смещения электронов в атоме, под действием поля световой волны. На электрон, находящийся в атоме действует также силы: квазиупругая – из-за наличия связи электрона с ядром:
сила сопротивления
Вынуждающая сила со стороны световой волны
Под действием этих сил электрон начинает совершать вынужденные колебания
Для простоты рассмотрения будем пренебрегать затуханием колебаний. В этом случае
Если учесть затухание (β ≠ 0), то мы получаем формулу, которая даёт хорошее соответствие с экспериментальной кривой)
|

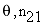
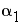 - угол падения. Тогда
- угол падения. Тогда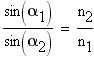
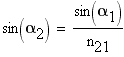
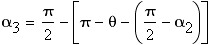
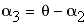


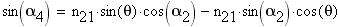
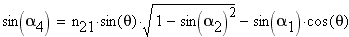
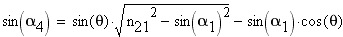
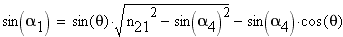
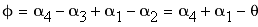


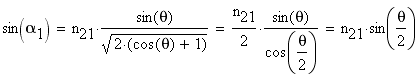

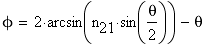

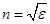 , при μ = 1.
, при μ = 1. , а в действительности n в =1,33. Такое противоречие между теорией Максвелла и экспериментом возникает вследствие того, что мы правильно применяем формулу ε0 = 81, которая справедлива только в статическом поле (ω = 0). Молекулы воды постоянно ориентируются в переменном электрическом поле. Электрическое поле световой волны изменяется по гармоническому закону.
, а в действительности n в =1,33. Такое противоречие между теорией Максвелла и экспериментом возникает вследствие того, что мы правильно применяем формулу ε0 = 81, которая справедлива только в статическом поле (ω = 0). Молекулы воды постоянно ориентируются в переменном электрическом поле. Электрическое поле световой волны изменяется по гармоническому закону.
 при μ = 1.
при μ = 1.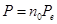
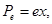
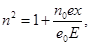

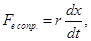
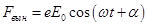
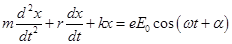
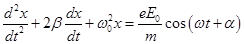
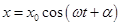
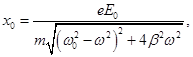
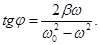
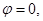
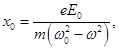
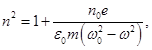
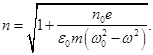
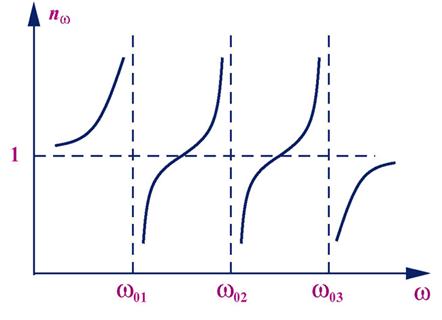 Из последней формулы видно, что n зависит от частоты падающего света, так же как и ε. Если ω0 > ω, то n существует, если ω0 = ω, то n терпит разрыв 2-го рода. В том случае, если атом содержит несколько валентных электронов:
Из последней формулы видно, что n зависит от частоты падающего света, так же как и ε. Если ω0 > ω, то n существует, если ω0 = ω, то n терпит разрыв 2-го рода. В том случае, если атом содержит несколько валентных электронов: