Геометрия ортогональных проекций плоскости

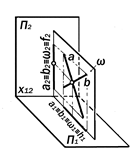
Общие положения

Плоскость является системой ком-планарных точек и линий. Она задаётся этими её элементами и простирается в двух взаимно-перпендикулярных напра-влениях до бесконечности. Эвклидова плоскость бесконечна и безгранична и поэтому всю её изобразить невозмож--но.

Проективная плоскость (см. глава 2, определение 2.14) также бесконечна, но концептуально гранична, ибо она замкнута по бесконечно-удалённой прямой, которая, в частности, у любой горизонтальной плоскости зрительно воспринимается как линия горизонта или граница, на которой «земля схо-дится с небом». Другими словами, про-ективная плоскость подобна сфере бес-конечно большого радиуса и поэтому всю её изобразить также невозможно.

Практически плоскости изображают-ся элементами их определителей, т.е., следующими системами компланарных точек и линий:

1. a (А,В,С) - тремя неколлинейны-

ми точками;

2. b (А, а) - точкой и неинцидент-

ной ей прямой;

3. g (а || b) - двумя параллельны-

ми прямыми;

4. d (a´b) - двумя пересекающими-

ся прямыми;

5. s (D ABC) - плоской фигурой;

6. t (f₂° ´ h₁°) - следами;

7. w (O) - плоской фигурой.

Все способы задания плоскостей геометрически равноценны, так как могут взаимно перезадаваться.

 

9.7.1. Геометрические модели плоскостей в системе двух плоскостей проекций

По отношению к плоскостям проек-ций П₁ и П₂ изображаемые плоскости могут занимать частные и общее поло-жение.

Частные положения плоскостей де-лятся на проецирующие и уровня.

Определение 9.5 Плоскости, пер-пендикулярные к плоскостям проек-

ций, называются п р о е ц и р у ю щ и-

м и (рис. 9.19 – 9.22):

a ^ П₁ – горизонтально-проеци-рующая плоскость;

b ^ П₂ – фронтально-проециру-ющая плоскость;

g ^ П₃ – профильно-проециру-ющая плоскость.

Определение 9.6. Плоскости, па-раллельные плоскостям проекций, на-зываются п л о с к о с т я м и у р о в-н я (рис. 9.23 – 9.25).

s || П₁ – горизонтальная плоскость

уровня;

t || П₂ – фронтальная плоскость

уровня;

w || П₃ – профильная плоскость уро-

вня.

Плоскости уровня занимают в про-странстве дважды частное положение, так как будучи параллельными к одной из плоскостей проекций, они перпен-дикулярны к другой и поэтому облада-ют всеми свойствами проецирующих плоскостей.

 

Рис.9.25.. Геометрическая модель про-

фильной плоскости уровня

 

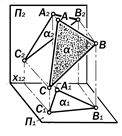
Определение 9.7. Плоскости, расположенные в пространстве про-извольно, т.е., не параллельно и не перпендикулярно ни к одной плоско-сти проекций, называются п л о с к о- с т я м и о б щ е г о п о л о ж е н и я

(рис. 9.26.).

Рис. 9.26. Геометрическая модель

плоскости общего положения

 

 

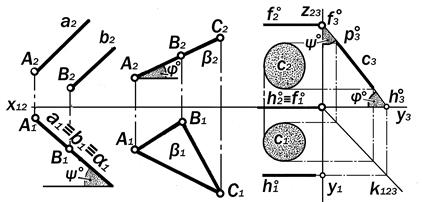
Рис.9.27. Графические модели

проецирующих плоскостей