Следы прямых. Определение 9.4. Точки пересе-чения изображаемых прямых с плоско-стями проекций называются с л е д а- м и прямых (см

Если прямые не параллельны пло-скостям проекций, то они с ними пере-секаются.

Определение 9.4. Точки пересе-чения изображаемых прямых с плоско-стями проекций называются с л е д а- м и прямых (см. п.5.1,определение 2.10).

Следы прямых бывают горизонта-льными,фронтальными и профильны-ми, в зависимости от того, с какими плоскостями проекций эти прямые пе-ресекаются. Основным позиционным свойством следов прямых линий яв-ляется их двойная природа, ибо они одновременно принадлежат и плоско-сти проекций и самой прямой, т.е., сами себя изображают. Отсюда следует, что построение следа прямой равносильно построению соответствующей проекции одной её точки.

Совершенно очевидно, что в си-стеме двух плоскостей проекций линии уровня и проецирующие прямые имеют по одному следу, а прямые общего положения, – по два.

 

9.2. Графические модели линий уровня и их изобразительные свойства (рис.9.4 – 9.6)

Так как прямая линия задаётся дву-мя нетождественными точками, то для её изображения достаточно изобразить эти точки и соединить их одноименные проекции под линейку.

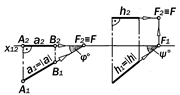
Рис.9.4. Графические модели горизонтальных прямых

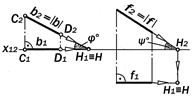
Рис.9.5. Графические модели фронтальных прямых

 

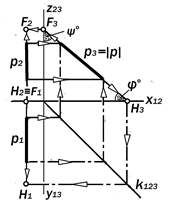
Рис.9.6. Графическая модель профильной прямой

 

 

Рис. 9.7. Графические модели проеци-рующих прямых

 

 

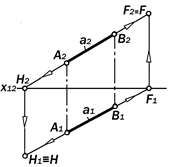
Рис.9.8. Графическая модель прямой общего положения

Одной из таких точек может быть след линии уровня, а если прямая об-щего положения, то обе точки могут быть её разноименными следами.

Для построения следов прямых ли-ний необходимо графически промоде-лировать два их позиционных свой-ства:

1. принадлежность следа к изобра-жаемой прямой и

2. принадлежность следа к плоскос-ти проекций.

Так как след принадлежит плоскости проекций, то одна из его проекций обя-зательно принадлежит оси проекций. Эта первая проекция следа строится как точка пересечения с осью той про-екции прямой, которая ей не парал-лельна. Вторая проекция следа строит-ся в проекционной связи с первой на второй проекции прямой, которая мо-жет быть параллельной или не парал-лельной оси проекций (см. рис.9.1- 9.5).

 

Изобразительные свойства проекций линий уровня

Позиционные свойства:

(в осной системе) (в безосной системе)

1. а Î П₁ Þ а₂ Î х₁₂; ¾

2. b ÎП₂ Þ b₁ Î х₁₂; ¾

3. h || П₁ Þ h ₂ || x₁₂; h || П₁ Þ h₂ ^ A₂A₁;

4. f || П₂ Þ f₁ || x₁₂; f || П₂ Þ f₁^ A₂A₁;

5. p || П₃ Þ(р₁ º А₂А₁ p || П₃ Þ р₁ º

º р₂)^ х₁₂; º А₂А₁ º р_2..

 

 

Утверждение 9.1. Горизонталь-ность одной из проекций прямой линии является графическим признаком то-го, что изображенная прямая являет-ся линией уровня.

Метрические свойства проекций

прямых линий

Метрическими характеристиками прямой линии является натуральная величина расстояния между двумя её точками и натуральные величины углов её наклона к плоскостям проек-ций.

Так как линии уровня параллельны плоскостям проекций, то они проециру-ются на них в свою натуральную ве-личину. По этой же причине угол на-клона прямой к той плоскости проекций,

по отношению к которой она не парал-лельна, проецируется в натуральную величину на ту плоскость проекций, по отношению к которой она параллельна:

1. h || П₁ Þ h₁ = | h |;

2. f || П₂ Þ f ₂ = | f |;

3. c ^ П₁ Þ с || П₂ Ù с₂ = | c |;

4. d ^ П₂ Þ d || П₁ Ù d₁ = | d |;

5. p || П₃ Þ р₃ = | p |;

6. h || П₁ Þ h₁ ^ x₁₂ = j ° = | h ^ П₂ |;

7. f || П₂ Þ f₂ ^ x₁₂ = y ° = | f ^ П₁ |;

8. c ^ П₁ Þ с ^ П₁ = 90°;

9. d ^ П₂ Þ d ^ П₂ = 90°;

10. р || П₃ Þ р₃ ^ z₂₃ = j° = | p ^ П₂ | Ù

Ù p₃ ^ y₃ = y° = | p ^ П ₁ |.