Графические модели плоскостей общего положения и их

Так как плоскости общего положе-ния не являются проецирующими, то ни одна из их проекций не является вы-рожденной в прямую линию и поэтому не обладают собирательным свойст-вом.

Так как плоскости общего положе-ния не являются плоскостями уровня,

то ни одна из проекций их плоских фи-

гур не конгруэнтна этим фигурам.

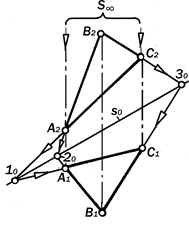
Отсюда следует, что комплексные

чертежи плоскостей общего положения не содержат непосредственной инфо-рмации о метрических характеристиках изображенных плоских фигур, опреде-ляющих их конкретное общее положе-ние.

Для определения этих характе-ристик необходимо графически решить соответствующие метрические задачи путем преобразования проекций фигу-ры общего положения в проекции этой же фигуры, но занимающей такое ча-стное положение, изображение кото-рого будет непосредственно содержать искомую метрическую информацию.

Рассматривая комплексный чертёж плоской фигуры, в частности, треуголь-ника АВС (рис. 9.30), обращаем вни-мание на то, что соответственные раз-ноименные проекции его вершин А, В и С лежат на параллельных, т.е., пересе-

Рис. 9.30. Двухкартинный комплексный чертеж плоской фигуры как дезаргова конфигурация

кающихся в бесконечно-удалённой точ-ке S_¥ линиях связи, а при продолжении его соответственных сторон убежда-емся, что они пересекаются в точках 1₀, 2₀, 3₀, лежащих на одной прямой s₀.

Отсюда следует вывод: Двухкар-тинный комплексный чертёж плоской фигуры является графической конс-трукцией, удовлетворяющей услови-ям теоремы Дезарга, а поэтому раз-ноименные проекции этой фигуры перспективно-аффинны или родст-

венны, т.е., являются гомологичными

фигурами.

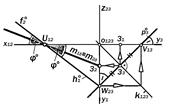
Рис.9.31. Положительно равнонаклонённая плоскость

Рис.9.32. Отрицательно равнонаклонённая плоскость

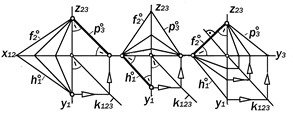
Рис9.33. Графическая модель положительно равнонаклонённой плоскости

Рис.9.34. Графическая модель отрицательно равнонаклонённой плоскости

Рис.9.35. Изобразительные свойства отогональных проекций равнонаклонённых плоскостей

Другими словами, двукартинный комплексный чертёж плоской фигуры задаёт на картине гомологию, т.е.,даёт возможность по заданной проек-ции строить ей соответственную по гра-фическим законам теоремы Дезарга.

Двухкартинный комплексный чер-тёж треугольника АВС как графическая конструкция интересен тем, что эле-ментами его структуры являются 10 то-чек (S_¥, А₁, А₂, В₁ В₂, С₁, С₂, 1₀, 2₀, 3₀) и 10 прямых (А₁А₂, В₁В₂, С₁С₂, А₁В₁ А₂В₂, В₁С₁, В₂С₂, А₁ С₁ , А₂С₂, s₀), которые так взаимосвязаны отношениями инциден-тности, что через каждую точку прохо-дят по три прямые, а на каждой прямой лежит по три точки.

Такая закономерная графическая конструкция называется к о н ф и г у – р а ц и е й Д е з а р г а и она справедлива не только в плоскости, но и в пространстве.