Графические модели

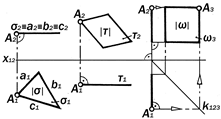
плоскостей различного положения в пространстве и их изобразительные свойства

Графические модели проецирующих плоскостей и их изобразительные свойства (рис.9.27)

Если плоскость является проециру-ющей, то она проходит через центр про-ецирования и, будучи перпендикуляр-ной к соответствующей плоскости про-екций, проецирует себя на неё в пря-мую линию. Так как эта прямая изобра-жает в с ю плоскость с её инциденция-ми, то с ней совпадают или на ней соби - раются проекции всех точек и линий этой плоскости.

Определение 9.8. Способность вырожденной в прямую линию проек-ции проецирующей плоскости приво-дить в тождественное расположение соответствующие проекции компла-нарных точек и линий называется её

с о б и р а т е л ь н ы м свойством.

Утверждение 9.13. Прямолинейно-сть одной из проекций изображаемой плоскости является графическим при-знаком того, что эта плоскость прое-цирующая.

Метрические свойства проекций проецирующих плоскостей

Так как проецирующие плоскости не параллельны ни одной из плоскостей проекций, то проекции их плоских фигур не могут быть им конгруэнтны. Другими словами, на комплексном чертеже про-ецирующей плоскости нет непосред-ственно й информации о натуральном виде её плоских фигур.

Так как проецирующие плоскости с

одной из плоскостей проекций состав-ляют прямой угол и поэтому проециру-ются на неё в прямую линию, то с этой прямой и осью проекций совпадут соответствующие проекции линейного угла как меры того двугранного угла, который составляется изображаемой плоскостью и той плоскостью проекций, к которой она не перпендикулярна.

 

Утверждение 9.14. Величина ли-нейного угла между вырожденной про-екцией изображенной плоскости и осью проекций метрически равна на-туральной величине угла наклона этой плоскости к той плоскости про-екций, к которой она не перпендику-лярна.

Отсюда следует, что комплексные чертежи проецирующих плоскостей содержат в себе непосредственную информацию о величинах двугранных

углов между ними и не перпендикуляр-

ными к ним плоскостями проекций.

 

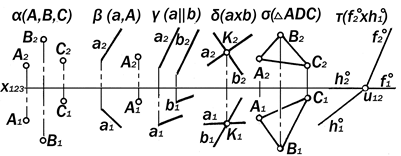
Рис.9.28. Графические модели плоскостей

уровня

Графические модели плоскостей уровня и их изобразительные свойства (рис.9.28)

Будучи проецирующей, плоскость уровня на одной плоскости проекций изображается в виде прямой линии, па-раллельной оси проекций (или пер-пендикулярной к вертикальной линии связи), а на второй – в поле точек, конгруэнтное её точечному полю.

s|| П₁ Þ s₂ ^ А ₂ А₁, s₁ = |s |;

t || П₂ Þ t₁ ^ А₂ А₁, t ₂ = | t |;

w || П₃ Þ w₁, w₂ º А₂ А_{1 ,} w₃ = | w |.

Это значит, что её вырожденная проекция обладает собирательным

свойством, а невырожденная изобра-жает все её конструктивные элементы в натуральную величину.

 

 

Рис.9.29. Графические модели

плоскостей общего положения

Метрические свойствапроекций

плоскостей уровня

Особенности метрических свойств

проекций плоскостей уровня определя-

ются особенностями их позиционных

свойств.

Так как эти плоскости параллельны одним плоскостям проекций и перпен-дикулярны к другим, то с одними они составляют углы в 0°, а с другими - 90°,т.е.:

s || П₁ Þ Ð s, П₁ = 0 °, Ð s, П ₂ = 90 °;

t || П₂ Þ Ð t, П ₂ = 0 °, Ð t, П₁ = 90 °;

w || П₃ Þ Ð w,П ₃ = 0 °, Ð w, П₁ Ù

Ù Ð w,П ₂ = 90 °.

Способность плоскостей уровня проецироваться на параллельные им плоскости проекций в натуральную ве-личину даёт возможность непосредст-венных измерений проекций для опре-деления метрических характеристик изображенных плоских фигур (их раз-меры, углы и расстояния между их эле-ментами, а также их площади).

Утверждение 9.15. Комплексные чертежи плоскостей уровня содержат в себе непосредственную информацию о позиционных и метрических свойст-вах изображенных плоских фигур.