Графические модели прямых общего положения и их изобра-зительные свойства

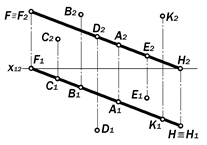
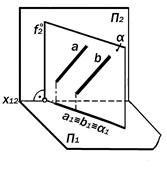
Если обе проекции прямой явля-ются прямыми, не параллельными и не перпендикулярными к осям проекций или вертикальным линиям связи, то изображенная ими прямая занимает в пространстве общее положение (рис. 9.8).

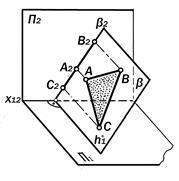
Рис9.9. Геометрическая модель идеи способа прямоугольного треугольник

Рис.9.10. Правило прямоугольного

треугольника

Если отрезок прямой не параллелен плоскости проекций, то длина его орто-

гональной проекции на эту плоскость не равна длине самого отрезка, а мень-ше неё на косинус угла его наклона к этой плоскости.

Из рис 9.9. видно, что отрезок АВ является ребром некоторого тетраэдра АВСD, по которому пересекаются две его грани в виде прямоугольных тре-угольников АВС и АВD, катеты ВС и АD которых являются соответственно гори-зонтальной и фронтальной линиями уровня, метрически равными горизонта-льной и фронтальной проекциям отрез-ка АВ.

Углы между гипотенузой АВ и прилежащими катетами ВС и АD метрически равны натуральным величинам углов

наклона отрезка АВ к П₂ и П_1, а длина гипотенузы АВ этих треугольников равна длине отрезка АВ общего положе-ния. Для графического по-строения гипотенузы пря-моугольного треугольника не-обходимо иметь два его кате-та. Информация о этих катетах непо-средственно присутствует на комплек-сном чертеже. Ведь прилежащий к углу наклона катет равен данной проекции отрезка, а противолежащий равен раз-ности расстояний другой его проекции до оси проекций.

Отсюда вытекает правило прямо - угольного треугольника для опреде-ления длины отрезка прямой общего положения и величин углов его наклона к плоскостям проекций по его ортого-нальному комплексному чертежу (рис. 11.9):

Натуральной величиной отрезка

прямой общего положения является длина гипотенузы прямоугольного треугольника, одним из катетов ко-торого является одна из проекций этого отрезка, а второй катет ме-трически равен разности расстояний концов другой его проекции до оси про-екций.

Натуральной величиной угла j ° на-клона отрезка АВ к плоскости П₁ явля-ется значение угла между горизонталь-ной проекцией отрезка и его натураль-ной величиной.

Натуральной величиной угла y ° на-

клона отрезка АВ к плоскости П₂ явля-

ется значение угла между фронтальной проекцией отрезка и его натуральной величиной.

Утверждение 9.4. Ортогональ-ные проекции отрезка прямой обще-го положения не содержат в себе не-посредственной информации о его метрике, но содержат все необходи-мые данные для её определения.

Два возможных варианта систем из точек и одной прямой

1. А, В, С,…Î а; 2. А,В,С,…Ï а.

Рис.9.11. Геометрическая модель

системы из точек и прямой

Точка, не принадлежащая прямой, может быть над, под, перед, за, правее, правее и выше (ниже, дальше, ближе) и левее (ниже, дальше, ближе) этой пря-мой.

Утверждение 9.5. Если точка принадлежит прямой, то одноимен-ные проекции этой точки и этой пря-мой инцидентны (рис. 9.12)

А Î а Þ А₁ Î а₁, А₂ Î а₂.

Рис.9.12. Графическая модель системы из точек и прямой

Утверждение 9.6. Если точка не при-

надлежит прямой, то одна или обе её проекции не принадлежат соответст-вующим проекциям этой прямой (рис. 9.12).

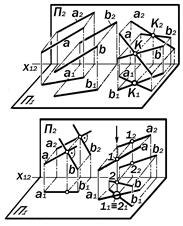
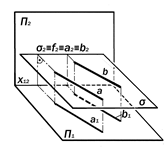
Рис.9.13. Геометрические модели

систем из двух прямых

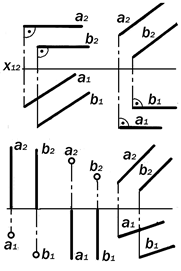
Рис. 9.14. Графические модели двух параллельных прямых

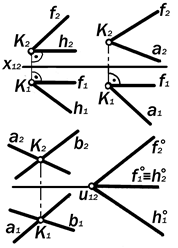
Рис. 9.15. Графические модели двух пересекающихся прямых

А Ï а Þ А₁ Ï а₁, А ₂ Ï а ₂;

А Ï а Þ А₁ Î а₁, А ₂ Ï а _{2 ;}

А Ï а Þ А₁ Ï а₁, А ₂ Î а _2.

9.6. Геометрические модели систем из двух прямых (рис. 9.13)

1. а || b; 2. с ´ d = K;

3. a ^ b;4. a @ b.

Относителтьно друг друга прямые мо-гут быть параллельными, пересекаю-щимися, в том числе, и под прямым уг-лом, и скрещивающимися.

Относительно плоскостей проекций прямые этих систем могут занимать как частные, так и общее положение.

1. Параллельные прямые (рис.9.14):

1.1. (a || П₁) || (b || П₁ );

1.2. (a || П₂) || (b || П₂);

1.3. (a ∦ П₁; П₂) || (b ∦ П₁; П₂).

Утверждение 9.7. Если две прямые в пространстве параллельны, то их одноименные проекции параллельны.

a || b Þ a₁ || b₁, a₂ || b ₂.

2. Пересекающиеся прямые (рис 9.15):

2.1. (h || П₁) х (f || П ₂ ) = K;

2.2. (a ∦ П₁) x (f || П₂) = K;

2.3. (a ∦ П₁, П₂) x (b ∦ П₁, П₂) = K.

2.4. (h Î П₁) x (f Î П₂ ) = u_12.

Утверждение 9.8. Если прямые в пространстве пересекаются, то их одноименные проекции также пересе-каются, а разноименные проекции то-чки их пересечения лежат на одной вертикальной линии связи.

3. Перпендикулярные прямые

(рис. 9.16)

3.1. (а || П₁) ^ (b || П₁) = А;

3.2. (a ⊥ П₁) ^ (b ^ П₁) = K;

3.3. (m || П₁) ^ (n || П₁) = L;

3.4. (a || П₂) ^ (b || П₂) = N;

3.5. (l || П₂ ) ^ (k || П₁) = K;

3.6. (c || П₂) ^ (d ∦ П ₂) = K;

3.7. (a ^ П₁) ^ (b ^ П₂) = K;

Рис.9.16. Графические модели взаимно-перпендикулярных прямых

Геометрическая модель системы из двух взаимно-перпендикулярных пря-мых предполагает такие 7 вариантов их расположения в пространстве, когда прямой угол между ними проецируется в прямой угол между их проекциями (рис.9.16).

Утверждение 9.9. Прямой угол проецируется в натуральную величи-ну на ту плоскость проекций, по отно-шению к которой либо обе его сторо-ны, либо одна из них параллельна.

Изобразительной особенностью комплексного чертежа прямого линей-ного угла является наличие на нем двух прямых углов. Один между одной из проекций его стороны -- линии уровня и вертикальной линией связи, второй, – собственно изображаемый угол.

8- й вариант расположения

сторон прямо-

го угла пред-

полагает их

общее поло-

жение. В этом

случае пря-

мой угол бу-

Рис. 9.17. Угол междудет проециро-

прямыми а и b непрямой ваться в ту- или острый, но не в прямой (рис. 9.17).

Рис. 9.18. Графические модели двух

скрещивающихся прямых

 

 

Рис. 9.19. Геометрическая модель горизонтально-проецирующей плоскости

Отсюда следует утверждение 9.10:

Если между одноименными проекциями двух пересекающихся прямых прямые углы, то изображенный угол между этими прямыми в пространстве не яв-ляется прямым.

Задача на построение проекций прямого угла со сторонами общего по-ложения является позиционной, тре-бующей выполнения последовательных графических операций, и поэтому будет рассмотрена выше (см. рис.10.35).

4. Скрещивающиеся прямые (рис.9.18).

 

Для того, чтобы прямые в прост-ранстве скрещивались, необходимо на-рушить в их расположении условия параллельности и пересечения.

4.1. (a || П₁) ∸ (b || П₁);

4.2. (a ⊥ П₃) ∸ (b ∦ П₁, ∦ П₂ );

4.3. (a – о.п.) ∸ (b || П₁);

4.4. (a – о.п.) ∸ (b – о.п.);

4.5. (a || П ₁) ∸ (b ⊥ П₁);

4.6. (a || П₁) ∸ (b ⊥ П₂).

Это означает, что на их комплекс-ных чертежах должны отсутствовать графические признаки таких располо-жений. (см. утверждения 9. 7 и 9. 8).

 

Утверждение 9.11. Если прямыев пространстве скрещиваются, то их одноименные проекции в общем случае пересекаются, но разноименные про-екции точек их пересечения не лежат на одной вертикальной линии связи.

Возникает вопрос: что изображаютточки пересечения одноименных проек-ций двух скрещивающихся прямых?

Ответ: Они изображают такие две точки на этих прямых, которые лежат на одном проецирующем луче.

 

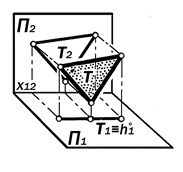
Определение 9.4. Точки двух скре-

щивающихся прямых, лежащие на од-ном проецирующем луче, называются к о н к у р и р у ю щ и м и.

На основе анализа взаимного рас-положения конкурирующих точек двух скрещивающихся прямых определяют

видимость этих прямых в составе не-

сквозных пространственных систем.

Пример 9.1.: Определить проекции не-видимых рёбер тетраэдра (рис.9.20).

 

Рис.9.20. Анализ положения конкурирующих точек

 

Анализ условия: На горизонтальной проекции тетраэдра пересекаются проек-ции скрещивающихся рёбер АD и ВС в точке, где 1₁ º 2₁;

На фронтальной проекции тетраэдра пересекаются проекции скрещивающихся прямых АС и ВD в точке, где 3₂ º 4₂.

Решение: 1. Определив фронтальные проекции 1₂ и 2₂ конкурирующих точек 1 и 2 на рёбрах ВС и АD, видим, что точка 1 на ребре ВС дальше от П₁, чем точка 2 на ребре АС и поэтому на виде сверху про-екция В₁С₁ будет видимой, а проекция

А₁D₁ - невидимой.

2. Определив горизонтальные проек-ции 3₁ и 4₁ конкурирующих точек 3 и 4 на рёбрах АС и ВD, видим, что точка 3 на ре-бре АС дальше от П₂ , чем точка 4 на ребре АС и поэтому на виде спереди проекция А₂D_2, будет видимой, а проекция А₂С₂ - невидимой.

 

Утверждение 9.12. На комплек-сном чертеже непрозрачного гранного объекта видимыми будут те проекции его скрещивающихся рёбер, конкуриру-ющие точки которых расположены в пространстве дальше от соответст-вующих плоскостей проекций.

Это происходит потому, что, распо-лагаясь по направлениям проециро-вания дальше от плоскостейпроекций, они закрывают собой те конкурирующие точки, которые ближе к этим плоскос-тям и поэтому невидимы. Определение видимости проекций элементов на чер-тежах пространственных систем обяза-тельно.

 

Рис. 9.21. Геометрическая модель фронтально-проецирующей плоскости

 

 

Рис.9.22. Геометрическая модель профильно-проецирующей плоскости

 

Рис.9.23. Геометрическая модель горизонтальной плоскости уровня

 

Рис.9.24. Геометрическая модель фронтальной плоскости уровня