Виды индексов по степени охвата элементов совокупности: индивидуальные и сводные.
Виды индексов по базе сравнения. Когда рассматриваются сопоставления уровней изучаемого явления во времени, то говорят о динамических индексах, в пространстве – о территориальных индексах и т. д. Динамические индексы бывают базисные и цепные. Территориальные индексы применяются для межрегиональных сравнений, а также в международной статистике при сопоставлении показателей социально-экономического развития различных стран. Виды индексов по степени охвата элементов совокупности: индивидуальные и сводные. Индивидуальные индексы служат для характеристики соотношения уровней только одного элемента совокупности, например рост или падение цен на какой-либо продукт. Индивидуальные индексы по существу являются относительными величинами динамики, выполнения плана или сравнения, и индексами их можно назвать только в широком смысле. Индекс, как относительный показатель, выражается в виде коэффициентов, когда база сравнения принимается за единицу, и в процентах, когда база для сравнения принимается за 100. Расчеты индивидуальных индексов просты по своей сущности и выполняются путем вычисления отношения двух индексируемых величин. Можно выделить: а) индивидуальный индекс цен, который показывает относительное изменение уровня цены по каждому виду продукции в отчетном году по сравнению с базисным:
б) индивидуальный индекс физического объема, характеризующий изменение объемов производства или реализации в натуральном выражении по каждому виду продукции во времени, в пространстве и плана, если фактический выпуск сравнивать с плановым заданием:
в) индивидуальный индекс выручки, отражающий динамику средств, полученных от реализации отдельных видов продукции:
Индивидуальные индексы выручки можно найти и через взаимосвязь индексов:
Пример. Рассмотрим подробнее индивидуальные индексы с учетом условных данных о ценах и реализации продукции за два периода:
При определении по данным таблицы статистических индексов Ш квартал принимается за базисный период, в котором цена единицы товара обозначается p0, а количество – q0. IV квартал принимается за текущий или отчетный период, в котором цена единицы товара обозначается p1, количество – q1. Тогда индивидуальные индексы составят: • цен:
В IV квартале цены увеличились по всем видам представленной продукции: на молоко – на 3,06 %, на яйца – на 1,12 %, на картофель – на 7,22 %; • физического объема:
Количество проданного молока в IV квартале снизилось по сравнению с III на 9,33 % (90,67% – 100 %), объем продажи яиц повысился на 8,28 %, а объем реализации картофеля сократился на 31,86 %; • товарооборота:
В IV квартале по сравнению с III выручка от реализации молока снизилась на 6,56 %, яиц – выросла на 9,5 %, картофеля – снизилась на 26,95 %. Если необходимо получить характеристику изменения изучаемого явления во всех последующих периодах по сравнению с первоначальным, то вычисляются базисные индексы. Они имеют постоянную базу сравнения, в качестве которой принимаются данные какого-то одного периода (при анализе динамики), какой-то территории (при территориальных сравнениях) и планового задания (при анализе выполнения плана). Например, сопоставление денежных доходов на душу населения II, III и IV кварталов с I кварталом. В случае, когда требуется охарактеризовать последовательное изменение изучаемого явления из периода в период, вычисляются цепные индексы. Они представляют собой сравнения текущих уровней с предшествующим уровнем или непрерывно меняющейся базой сравнения. Например, при изучении денежных доходов на душу населения по кварталам года сопоставляют денежные доходы II квартала с I кварталом, III квартала – со II кварталом и IV квартала – с III кварталом. В зависимости от задачи исследования и характера исходной информации базисные и цепные индексы исчисляются как индивидуальные (однотоварные), так и общие. Способы расчета индивидуальных базисных и цепных индексов аналогичны расчету относительных величин динамики. Таблица – Система индивидуальных индексов
Между цепными и базисными индивидуальными индексами существует взаимосвязь, которая позволяет переходить от одних индексов к другим. Отношение базисного индекса отчетного периода к базисному индексу предшествующего периода дает цепной индекс отчетного периода:
Произведение последовательных цепных индивидуальных индексов дает базисный индекс последнего периода:
Системы базисных и цепных индексов могут быть построены и для агрегатных индексов, только с использованием постоянных и переменных весов. В связи с тем, что индивидуальные индексы являются разновеликими по направлению и интенсивности изменения, возникает необходимость их обобщения при определении общего для данного ассортимента изменения цен и количества реализованных товаров. Для этого вычисляются соответствующие общие индексы. Общие (сводные) индексы отражают изменение всех элементов сложного явления и состоят из двух частей: индексируемой величины и соизмерителя, который называется «весом». Одна из особенностей сводных индексов состоит в том, что исследуемый показатель рассматривается не изолированно, а во взаимосвязи с другими показателями. Они имеют более сложную методику построения и расчета.
|


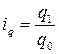

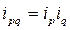
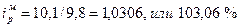








 ;
;  ;…
;… 
 ;…
;… 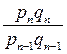
 ;
;  ;…
;… 
 ; …
; … 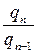
 ;
;  ; …
; … 
 ; …
; … 





