Агрегатные индексы цен Пааше, Ласпейреса и Фишера.
Агрегатная форма индексов цен, в которой изменение цен увязывалось с конкретной массой товаров, была введена в практику расчетов во второй половине XIX в. В 1864 г. немецкий экономист Э. Ласпейрес предложил индекс, который отражает изменение цен и строится по продукции базисного периода. Формула агрегатного индекса цен Ласпейреса представляет собой следующее отношение:
Индекс цен Ласпейреса показывает, во сколько раз товары базисного периода подорожали или подешевели в результате изменения цен на них в отчетном периоде. Эти особенности индекса Ласпейреса обусловливают его применение при прогнозировании объема товарооборота, в связи с намечаемыми изменениями цен на товары в предстоящем периоде. В 1874 г. немецкий экономист Г. Пааше впервые предложил агрегатный индекс цен с отчетными весами. Формула этого индекса выглядит следующим образом:
Индекс цен Пааше характеризует изменение цен отчетного периода по сравнению с базисным по товарам и услугам, реализованным в отчетном периоде, и фактическую экономию или перерасход от изменения цен. Кроме того, при построении общего индекса цен в качестве соизмерителей индексируемых величин (р1 и р0) могут применяться средние величины реализации товаров за два или большее число периодов. Разность числителя и знаменателя агрегатного индекса цен показывает, как в абсолютном выражении изменилась общая стоимость продукции за счет роста (сокращения) цен на продукцию:
Американский экономист И. Фишер предложил «идеальный» индекс, названный его именем, представляющий среднюю геометрическую из произведения двух агрегатных индексов цен Ласпейреса и Пааше:
Данную формулу можно использовать и для определения индекса физического объема. Идеальность формулы Фишера заключается в том, что индекс обратим во времени, т.е. не зависит от выбора базы сравнения. Недостаток же формулы в том, что она лишена конкретного экономического содержания (разность между числителем и знаменателем не показывает никакой реальной экономии или потерь вследствие изменения цен). Индекс Фишера в силу сложности расчета и трудности экономической интерпретации на практике используется довольно едко. Кроме того, многочисленные расчеты показали, что вполне можно применять не среднюю геометрическую, а среднюю арифметическую величину из индексов Ласпейреса и Пааше для получения осредненной величины индекса. Рассмотрим основные приемы применения индексного анализа на примере Пример. Имеются следующие данные о ценах реализации товаров, в руб.:
Определить: 1. агрегатный индекс цен на товары, взвешенный по продукции текущего периода (индекс Пааше) и по продукции базисного периода (индекс Ласпейреса), а также «идеальный» индекс Фишера; 2. агрегатный индекс физического объема продажи товаров и услуг в сопоставимых ценах по методикам Пааше и Ласпейреса; 3. агрегатный индекс товарооборота; 4. абсолютный прирост стоимости товаров вследствие изменения цен и объема продаж в целом по двум видам товаров. Решение. 1) Агрегатные индексы цен:
Таким образом, выполненные расчеты имеют разные показания индексов цен. Это объясняется тем, что индексы Пааше и Ласпейреса характеризуют качественные особенности изменения цен. В текущем периоде по сравнению с базисным наблюдался рост цен на товары А и Б на 16,9 % по формуле Ласпейреса, на 16,98 % – по формуле Пааше. Индекс Фишера дает осредненную величину повышения цены – 16,94 %. 2) Агрегатные индексы физического объема:
3) Агрегатный индекс выручки от реализации или товарооборота:
Для расчета агрегатного индекса выручки от реализации также можно воспользоваться любой из двух моделей:
4) Абсолютный прирост стоимости товаров:
• вследствие изменения цен:
Величина этого показателя характеризует перерасход средств населением вследствие изменения цен при покупке товаров данного ассортимента на 35500 руб. (по формуле Ласпейреса) и на 45000 руб. (по формуле Пааше) по ценам, повышенным на 16,9% или 16,98% соответственно; • вследствие изменения объема продаж:
Таким образом, выручка от реализации продукции вследствие изменения объема продаж увеличилась на 55000 руб. (по формуле Ласпейреса) и на 64500 руб. (по формуле Паше). -4- Средневзвешенный индекс – средняя величина из индивидуальных индексов. При его расчете используются две формы средних величин: арифметическая и гармоническая. Применение той или иной формулы средневзвешенного индекса зависит от имеющейся в распоряжении информации. Средний гармонический индекс цен применяется в тех случаях, когда неизвестны отдельные значения р1 и q1, но дано их произведение р1q1 и индивидуальные индексы цен iр = p1/p0, а сводный индекс должен быть исчислен с отчетными весами. Индивидуальные индексы должны быть взвешены таким образом, чтобы средний гармонический индекс совпал с агрегатным. Средний гармонический индекс цен:
Весами индивидуальных индексов в данном индексе является стоимость отдельных видов продукции отчетного периода в ценах того же периода р1q1.. Средний арифметический индекс цен получается в том случае, если из индивидуального индекса цен
Средний арифметического индекса физического объема продукции:
Средний гармонический взвешенный индекс физического объема продукции:
Средние индексы широко применяются для анализа состояния рынка ценных бумаг. Индикаторы рынка ценных бумаг рассчитываются по их видам: акции, облигации, опционы и др. Можно выделить следующие интегральные показатели: индексы Доу-Джонса, индекс Стендарта и Пура. Покажем особенность применения средних индексов на следующем примере. Пример. Потребление товаров и услуг населением района характеризуется следующими показателями:
Определить: 1) индивидуальные индексы цен и физического объема; 2) общий индекс на товары и услуги; 3) общий индекс физического объема продажи товаров и услуг в сопоставимых ценах; 4) общий индекс товарооборота. Решение 1) Индивидуальные индексы рассчитываются по формулам:
следовательно,
2) Тогда сводные индексы цен на товары и услуги, рассчитанные по формулам Паше и Ласпейреса с учетом индивидуальных индексов, составят:
или 121,8 %;
или 122,3 %. Во II квартале по сравнению с I кварталом наблюдался рост цен на все виды товаров и услуг на 21,8 % по формуле Пааше, на 22,3 % - по формуле Ласпейреса. 3) Сводные индексы физического объема на товары и услуги, рассчитанные по формулам Паше и Ласпейреса с учетом индивидуальных индексов, составят:
или 86,5 %
или 88,5 %. Таким образом, во II квартале по сравнению с I кварталом в целом имеет место снижение объема реализации продукции и услуг в натуральном выражении на 13,5 % по формуле Ласпейреса, на 11,5 % – по формуле Пааше. 4) Общий индекс товарооборота составит:
Индекс показывает, что стоимость товаров и услуг в среднем увеличилась на 6,68 %. -5- Для однородной совокупности возможно использование средних значений, общее изменение которых обусловлено взаимодействием двух факторов: изменением отдельных уровней показателя и изменением в структуре весов. Под изменением структуры здесь понимают изменение доли отдельных единиц совокупности, из которых формируются средние в общей их численности. Например, динамика среднедушевого дохода населения зависит от изменения среднего дохода каждого человека и от изменения количества людей с более высокими и низкими доходами в общей численности; средняя цена на хлеб может изменяться не только под влиянием изменения цены хлеба, но и в результате изменения состава товарной массы. Эта задача решается с помощью индексного метода, то есть путем построения системы взаимосвязанных индексов. Система включает три индекса: переменного состава, постоянного состава и структурных сдвигов. Индекс переменного состава представляет собой соотношение средних величин какого-либо признака в отчетном и базисном периодах:
Данный индекс характеризует не только изменение индивидуальных цен в местах продажи, но и изменение структуры реализации по предприятиям розничной и оптовой торговли, рынкам, городам и регионам. Индекс постоянного (фиксированного) состава характеризует динамику средней величины при одной и той же фиксированной структуре какой-либо однородной совокупности, то есть когда влияние структурного фактора устранено:
Индекс постоянного состава может быть рассчитан и в агрегатной форме:
Индекс структурных сдвигов необходим для измерения влияния только структурных изменений на исследуемый средний показатель и может быть рассчитан по формуле:
Индексы переменного, постоянного состава и структурных сдвигов увязываются в следующую систему:
Если в индексах средних уровней в качестве весов используются удельные веса единиц совокупности в общей численности совокупности, то есть показатели доли (d = f/Σf), то система индексов может быть записана в следующем виде:
Система индексов переменного, постоянного состава и структурных сдвигов строится для изучения динамики среднего уровня цен, себестоимости, фондоотдачи, рентабельности, производительности труда, заработной платы и других вторичных признаков. Помимо мультипликативной модели, на основе индексов переменного, постоянного состава и структурных сдвигов может быть построено и аддитивное разложение. Так, общий абсолютный прирост (уменьшение) среднего уровня признака в целом по совокупности находится по формуле:
Абсолютный прирост (уменьшение) среднего уровня признака в целом по совокупности за счет изменения значений изучаемого признака у отдельных единиц совокупности и за счет структурных изменений рассчитывается соответственно как разность числителей и знаменателей индексов постоянного состава и структурных сдвигов:
В общем виде аддитивное разложение имеет вид:
|

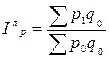


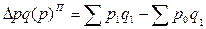





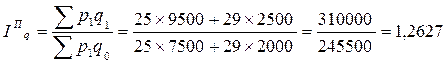

 руб.
руб. руб.
руб.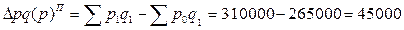 руб.
руб. руб.
руб. руб.
руб. , т.к.
, т.к.  , то
, то 
 , а затем подставить ее в числитель агрегатного индекса цен. Данный индекс тождествен агрегатному индексу Ласпейреса и имеет следующий вид:
, а затем подставить ее в числитель агрегатного индекса цен. Данный индекс тождествен агрегатному индексу Ласпейреса и имеет следующий вид:
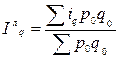









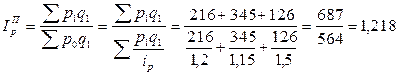



 , или 106,68 %.
, или 106,68 %.







 или
или 
 или
или 
 или
или 




