Подбор экспертов и формирование экспертных групп. Формирование вопросов и правил определения суммарных оценок экспертов.
Выделяются следующие основные этапы проведения экспертных опросов: 1. Подбор экспертов и формирование групп. 2. Формирование вопросов и составление анкет. 3. Формирование правил определения суммарных оценок на основе оценок отдельных экспертов. 4. Работа с экспертами. 5. Анализ и обработка экспертных оценок. 1 этап. Здесь, исходя из целей экспертных оценок, решаются вопросы относительно структуры экспертной группы, количества экспертов и их индивидуальных качеств, т.е. определяются направления (разработка новых товаров, ценообразование, сбыт и т.п.), по которым необходимо привлечь экспертов (устанавливается их специализация). Дальше по каждому направлению выделяются подгруппы экспертов, и устанавливается количество экспертов в каждой подгруппе, которое зависит от конкретной постановки задачи и должно обеспечить необходимый охват по каждому конкретному вопросу. Затем определяются требования к квалификации экспертов, стажу их работы в данной области опроса и общему стажу. На практике чаще используется «прагматический подход» определения численности экспертной группы. По данному подходу нижняя граница численности (Nmin) должна зависеть от числа оцениваемых событий (m) (например, данное правило соблюдается при работе ученых советов, комиссий специалистов и т.п.). Поэтому принимается условие Nmin ³ m. Верхней границей численности экспертной группы является потенциально возможное число экспертов (Nn). Nmax £ Nn, следовательно действительное значение численности группы N находится в пределах m £ Nmin £ N £ Nmax £ Nn. После этого определяется структура и состав группы, т.е. подбираются в группы эксперты требуемой специализации и квалификации, а для того чтобы событию была дана всесторонняя оценка, то число экспертов Ni каждого i-го направления желательно выбрать одинаковым
Дальше должно быть учтено ограничение, касающееся соответствия целей экспертов целям экспертных оценок, т.е. необходимо установить, есть ли тенденция у отдельных экспертов объективно оценивать рассматриваемые события. Для этого нужно выявить возможные потенциальные цели экспертов, противоречащие целям получения объективных результатов. Анализируя предшествующую деятельность экспертов, выясняют наличие причин, которые приводили к завышению или занижению оценок таким образом, чтобы это повлияло на групповые оценки в направлении желательном для этого эксперта или других лиц. Исходя из вышесказанного, последовательность формирования групп может быть следующей. Сначала определяется потенциально возможное число экспертов (Nn), затем минимально допустимая численность (Nmin). После этого среди потенциально возможных экспертов выделяют группу специалистов Nk (Nk £ Nn) требуемой квалификации. Затем из Nk исключают экспертов, у которых цели могут противоречить целям получения объективных результатов. Из оставшихся экспертов Nц (Nц £ Nk) формируют группы таким образом, чтобы обеспечить равное представительство. Для этого определяют вначале максимально возможное число представителей
Затем находят направление с наименьшим числом экспертов
2 этап. Формирование вопросов и составление анкет. Правила опросов экспертов должны обеспечить соблюдение ряда условий, таких как: - независимость формирования экспертами собственного мнения об оцениваемых событиях; - удобство работы с предлагаемыми анкетами (вопросы должны быть в общепринятых терминах и не содержать смысловую неоднозначность); - логическое соответствие вопросов структуре объекта опроса; - приемлемые затраты времени по вопросам анкеты, удобное время получения вопросов и выдачи ответов; - сохранение анонимности ответов; - проведение коллективных обсуждений оцениваемых событий; - представление экспертами требуемой информации. Для обеспечения выполнения этих условий должны быть разработаны правила проведения опроса и организации работы экспертной группы. 3 этап. Формирование правил определения суммарных оценок на основе оценок отдельных экспертов. В общем случае групповая оценка (ai) каждого события (Ci) зависят от оценок этого события экспертами, а также степени компетентности (hj) экспертов. Степень компетентности (hj) эксперта учитывает его опыт и квалификацию и является основной характеристикой эксперта, которая используется при определении групповых оценок, т.е. ai=f(aij; hj), где i=1;2;…m – количество событий, j=1;2;…p – количество экспертов. Обычно данную функцию представляют в виде
При равной компетентности экспертов эта формула принимает вид
В зависимости от специфики экспертных опросов, объекта исследования и используемой методики обработки экспертных данных оценки аij может иметь различную шкалу измерения: от 0 до 1; от 0 до 10; от 0 до 100. Выбор той или иной шкалы определяется удобством получения и обработки оценок, а также предпочтениями исследования. В связи с тем, что оценка компетентности эксперта, как и оценка самого эксперта, носит субъективный характер, то на практике часто используют вторую формулу в качестве интегральной оценки. Только при этом на этапе отбора экспертов большее внимание уделяют неформальной оценке уровня квалификации экспертов. 4 этап. Работа с экспертами. Работа с экспертами в основном содержит 3 этапа: На первом этапе эксперты привлекаются в индивидуальном порядке с целью: - уточнить модель объекта, ее параметры и показатели, подлежащие оценке; - уточнения формулировки вопросов и терминологии в анкетах; - согласования целесообразности представления таблиц экспертных оценок в той или иной форме; - уточнения состава группы экспертов. На втором этапе экспертам направляются анкеты с пояснительным письмом, в котором описывается цель работы, структура и порядок заполнения анкет с примерами. Третий этап работы с экспертами осуществляется после получения результатов опроса. На этом этапе от экспертов в форме консультаций получают всю недостающую информацию для уточнения полученных данных и окончательного анализа. 5 этап. Анализ и обработка экспертных оценок. При проведении анализа необходимо определить согласованность действий экспертов и достоверность экспертных оценок. Пусть для каждого события (Сi) на основании оценок аij, полученных группой из Р экспертов образованна матрица рангов важности - êêαij çç, где i=1;2;…m - число событий, j=1;2;…p – число экспертов. Матрица êêαij çç, получается из матрицы ççаijçç исходя из рангов важности событий, т.е. при ранжировании события располагаются в порядке увеличения или уменьшения какого либо признака (Х) и ранг aij указывает то место, которое занимает i-е событие среди других (m) событий, ранжированных в соответствии с признаком (Х). Ранжирование применяется, когда события располагаются согласно неизмеримому и не подсчитываемому качеству (например, потребительские свойства товара, направления совершенствования товара и т.д.) или рассматриваются только относительно взаимного расположения во времени или пространстве. Рассмотрим упорядоченную последовательность суммарных рангов m событий:
αi находится из матрицы êêαij çç по формуле
Приведем условный пример определения рангов важности событий исходя из их коэффициентов относительной важности (более важное событие имеет меньший ранг важности)
Среднее значение для суммарных рангов рассматриваемого ряда равно
Суммарное квадратическое отклонение (S) суммарных событий от среднего значения α равно
Величина S будет максимальна, если все Р экспертов дадут одинаковые оценки каждому событию (Сi). Тогда
Естественно, что в качестве меры согласованности экспертов принимается отношение S/Smax, тогда
где W – коэффициент конкордации. Его величина изменяется от 0 до 1. При W=0 согласованность мнений экспертов отсутствует, т.е. связи между оценками различных экспертов нет и наоборот, при W=1 согласованность мнений полная (однако это может говорить о сговоре экспертов). В том случае если последовательность (3) имеет еще и равенства, т.е. существует совпадение рангов, то формула для коэффициента конкордации имеет вид
где где Kj – число повторяющихся рангов в j -ом ряду. Когда ранги повторяются, то для получения нормальной ранжировки, необходимо приписать событиям, имеющим одинаковые ранги, равный среднему значению мест, которые эти события поделили между собой. Например, получена следующая ранжировка событий:
События 2 и 5 поделили между собой 2-е и 3-е места. Значит им приписывается ранг (2+3)/2=2,5. События 3, 4 и 6 поделили между собой 4-е, 5-е и 6-е места и им приписывается ранг (4+5+6)/3=5, таким образом получаем нормальную ранжировку:
|

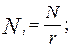 где r – число направлений; i = 1;2;3;… r.
где r – число направлений; i = 1;2;3;… r.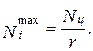
 , которое входит в группу Nц и затем уже численность группы будет определяться
, которое входит в группу Nц и затем уже численность группы будет определяться
 (1)
(1)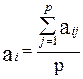 (2).
(2). (3);
(3);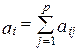 .
.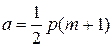 .
. .
.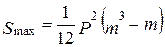 .
. ,
,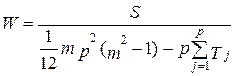 ;
; ;
; - число повторений каждого ряда в j -ом ряду;
- число повторений каждого ряда в j -ом ряду;


