Методы расчета предельных безводных и безгазовых дебитов несовершенных скважин, дренирующих нефтегазовые залежи с подошвенной водой
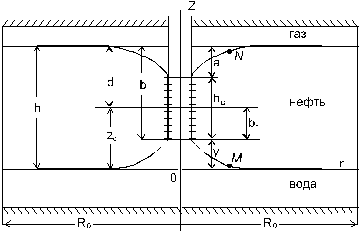
При разработке нефтегазовых залежей с подошвенной водой или нефтяных оторочек возникают гидродинамические задачи по определению предельных безводных и безгазовых дебитов, предельных депрессий, наивыгоднейшего интервала вскрытия нефтяной оторочки относительно ГНК и ВНК, безводного периода, безводной нефтеотдачи на момент полного обводнения или загазовывания скважин. Приближенная теория стационарных конусов применительно к подгазовым нефтяным залежам с подошвенной водой была впервые разработана М. Маскетом и И.А. Чарным. Дальнейшее развитие она получила в работах А.К. Курбанова, П.Б. Садчикова, А.П. Телкова, Ю.И. Стклянина, Р. Чанея, И. Лукерена и др. Формулы Мейера и Гардера и П.М. Шульги для определения предельного безводного и безгазового дебита исходят из теории безнапорного притока к несовершенной скважине и дают весьма приближенные завышенные против действительных предельных значения, т. к. они фиксируют дебиты уже в момент прорыва газа или воды. Рассмотрим приближенные, но более обоснованные методы [16]. 11.3.1. Методика расчета предельных безводных и безгазовых дебитов, основанная на гидравлической теории безнапорного притока. Схема одновременного существования конусов газа и воды показана на рис. 11.5. Пусть Н г, Н в, Н н есть гидравлические напоры в газовой, водяной и нефтяной зонах соответственно. Р г, Р в и Р н – пластовые давления в указанных зонах, а
Если эту точку переместить на контур скважины, то в соответствии с обозначениями на схеме имеем z=(h – b)+ h c. Решая совместно два уравнения, исключая
Аналогично для точки М, перемещенной на контур скважины, получаем:
Если поместить точки N и М на контур пласта, то получаем, соответственно, выражения
из которых следует
Решая совместно (11.7), (11.8) и (11.9), находим нижнее положение интервала перфорации, обеспечивающее критическое значение безводного и безгазового дебита при заданном значении h c
Рис. 11.5. Схема одновременного существования конусов газа и воды
|
– давление в некоторой точке на поверхности раздела газ-нефть и вода-нефть (см. рис. 11.5),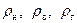 
- плотности нефти, воды и газа соответственно. Тогда относительно точки N можно записать следующее выражение:
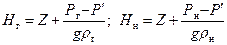. (11.6)
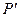и пренебрегая капиллярным давлением Р к= Р н– Р г, получаем:
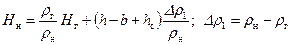. (11.7)
.
; 
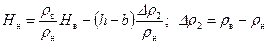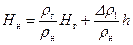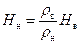, (11.8)
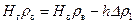. (11.9)
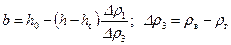. (11.10)
