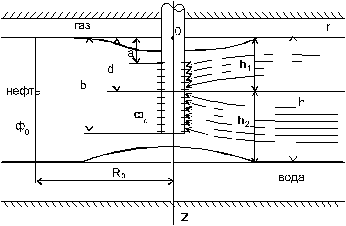
При безнапорном притоке к несовершенной скважине
Определим ординату z 0 нейтральной линии тока. Уравнения для напоров (11.5) и (11.6) относительно плоскости z 0 (см. рис. 11.5) записывается в виде:
Решая совместно (11.11) и (11.9), получаем
Расстояние b 1 от нижних отверстий перфорации до нейтральной линии тока, как это следует из схемы, есть
Таким образом, определив ординату нейтральной линии тока (горизонтальную плоскость) и заменив ее непроницаемой жесткой перегородкой, формально получаем два пласта. Дифференциальное уравнение безнапорного притока для верхнего пласта есть
Разделяя переменные и интегрируя (11.14) в пределах по r от r c до R 0 и по z от z 2 до z 1, где
получаем
Интегрируя уравнение для нижнего пласта
в пределах по r от r 0 до R 0 и по z от z 1=(z 0 –a) до z 2, получаем
Суммарный критический дебит Q = Q 1 + Q 2 определится формулой
Здесь принимаются следующие размерности: [ K r]=м2; [ h ]=м; [ Dr ]=кг/м3; [ m ]= Пример 1. Рассчитать интервал перфорации, положение нейтральной линии тока и предельный безводный и безгазовый дебит скважины, дренирующей нефтяную оторочку при следующих исходных данных: пласт горизонтальный однородно-изотропный, æ;*=1; условный контур питания R 0=200 м; толщина нефтяной оторочки h =25 м; проницаемость пласта K r=1,02×0,5×10—12 м2; вскрытая толщина h с=12,5 м; радиус скважины r c=0,1 м; вязкость нефти m н=2,5 мПа×с=10-3×2,5 кг/м∙с; разность плотностей жидкостей Dr 1=870 кг/м3, Dr 2=200 кг/м3, Dr 3=1070 кг/м3; скважина совершенная по характеру вскрытия. Расчеты, произведенные по формулам (11.10), (11.12), (11.13) и (11.19), дают следующие результаты: b =14,84 м; z 0=20,33 м; b 1=10,16 м; Q =9,87 м3/сут. Следовательно, а =2,34 м и y =10,17 м. Следует заметить, что полученный расчетный предельный дебит больше действительного предельного, т. к. формула (11.19) получена из условия «устойчивости» конусов уже при достижении ими вершин интервала перфорации. Строго говоря, устойчивость конусов при таком положении невозможна.
11.3.2. Потенциометрический метод расчета предельных безводных и безгазовых дебитов. Американские исследователи П. Чаней и др. [19], пользуясь аналитическим анализатором, разработали графический метод решения задачи по определению предельных безводных и безгазовых дебитов скважин для фиксированных характеристик пласта и жидкостей (интервал перфорации и его положения, радиус контура питания, проницаемость пласта, вязкость и плотность жидкостей и газа). Математические уравнения, составленные для определенной геометрии пласта, были преобразованы для пластовой системы с подобной геометрией. Графики рис.11.6, полученные таким образом [19] определяют зависимость предельного дебита как функцию расстояния от верхних дыр перфорации до ГНК – в случае верхнего газа, или до кровли пласта – в случае отсутствия его. Графики построены для следующих параметров пласта и жидкостей: R 0=305 м; r c=0,076 м; Kr =1 д =1,02×10-12 м2; m н=1 мПа×с; Dr 1=600 кг/м3; Dr 2=300 кг/м3, которые соответствуют пяти фиксированным нефтенасыщенным толщинам h: 3,8; 7,6; 15,25; 22,8; 30,5 м. Кривые А, В, С, D, Е и а, b, с, d, e соответствуют различным интервалам вскрытия: первые относятся к конусу воды, вторые – к конусу газа. Получены также решения и для R 0=152,5 м для различных толщин нефтяного пласта и интервалов вскрытия. При этом установлено, что предельный дебит при радиусе контура питания R 0=152,5 м на 10-15% больше, чем при R 0=305 м. Построенные графики оказалось возможным использовать для расчета предельных дебитов и при других характеристиках пластовых жидкостей и коллектора, но при прежней геометрии пласта. Подробный анализ приведенного метода с иллюстрацией расчетов на конкретных примерах изложен также в книге [9]. Ограниченность метода: не обладает универсальностью, не учитывает анизотропность пласта, трудность отсчета в полулогарифмических координатах, исключающих использование приведенных графических зависимостей в качестве рабочих графиков.
Рис. 11.6 (а,б). Зависимость предельного дебита Q (барели/сутки) отрасстояния а (футы) между верхними дырами перфорации и ГНК в случае верхнего газа или до кровли пласта в случае отсутствия его. Размеры в футах: а). hо = 12,5; А, В, С, D, Е — кривые для конуса воды;
Рис.11.6 в, г, д. исимость предельного дебита Q (барели / сутки) от расстояния а (футы); А, В, С, D, Е —кривые для водяного конуса; a, b, c, d, e — кривые для газового конуса. Размеры в футах: в) h 0 = 50; А, а -5; B, b 10; С, с - 15; D, d -20; Е, е - 25; г) h 0 = 75; А, а - 7,5; B, b - 15; С, с - 22,5; D, d -30; Е, е - 35,5; д) h 0 = 100; А, а 10; B, b - 20; С, с - 30; D, d -40; Е, е - 50. 11.3.3. Методика расчета одновременно предельных безводных и безгазовых дебитов Курбанова-Садчикова, основанная на теории напорного притока. При решении задачи авторы [20-22] исходили из основного допущения приближенной теории устойчивых конусов Маскета-Чарного, что отклонение поверхности двух жидкостей в пористой среде от начальной плоской формы не влияет на распределение потенциала скорости фильтрации в нефтяной зоне пласта, рассматривая нестационарное течение жидкостей как последовательную смену стационарных состояний. Область притока при этом условно разделяется на две части путем введения в поток непроницаемой горизонтальной плоскости, проходящей через середину интервала вскрытия пласта. таким образом, получается два самостоятельных пласта с соответствующими относительными вскрытиями (см. рис. 11.5), в котором может быть применен любой из существующих методов расчета предельных дебитов: относительно верхнего газа и подошвенной воды. Как указывают авторы [20-23] метод, основанный на таком искусственном разделении потока, может дать удовлетворительные результаты лишь в том случае, если в скважине действительно реализован интервал вскрытия, при котором предельное устойчивое состояние конусов газа и воды наступает одновременно, что на практике при неизменном положении интервала перфорации неосуществимо. Приняв за основу аналитическое решение М. Маскета для напорного притока к несовершенной по степени вскрытия пласта скважине, авторы разработали графический метод определения интервала вскрытия нефтяного пласта и предельных безводных и безгазовых дебитов. 11.3.4. Уточненная методика расчета одновременно предельных безводных и безгазовых дебитов. В основу решения этой задачи положена приближенная теория устойчивых конусов Маскета-Чарного. В отличие от предыдущего метода здесь используется аналитическое решение задачи о притоке к несовершенной скважине в однородно-анизотропном пласте, полученное в работах [9, 14, 24] для широкого диапазона параметра r, в том числе и для r <1, а условное разделение нефтяного пласта производится по нейтральной линии тока, метод отыскания которой, а также соответствующие расчеты и графические построения приведены в работах [9, 14, 25]. Кратко изложим суть этого метода. В работах А.П. Телкова и Ю.И. Стклянина [9, 14, 16] получено точное решение для распределения потенциала j (z, r, h) в однородно-анизотропном пласте с непроницаемой кровлей и подошвой, вызванного работой точечного стока интенсивностью q с координатами z = h и r =0. Принимая скважину за линейный сток с постоянным удельным расходом q = Q /(b – a), потенциал несовершенной скважины, вскрывшей пласт в интервале от z = a до z = b (рис. 11.7), выразится в виде
где Ф 0 – потенциал на контуре питания R 0. На рис. 11.7 представлена схема притока нефти к скважине, вскрывшей нефтяную оторочку, и показана картина линий тока при двухстороннем устойчивом конусообразовании. Очевидно, в этом случае в разрезе существует горизонтальная линия тока z=d, а плоский круг, описываемый этой линией, условно можно заменить жесткой непроницаемой перегородкой и считать течение в каждой части пласта самостоятельным и независящим от течения в другой области. Таким образом, формально получаем два цилиндрических пласта с непроницаемыми кровлей и подошвой, соответственно толщинами h 1= d и h 2= h – d (см. рис. 11.7). Величина вскрытия для первого (верхнего) пласта – (d – a), для второго – (b – d). Погонный расход каждой части скважины одинаков. Оба пласта имеют общий контур питания R 0; сверху образуется конус газа, снизу – конус воды. Дифференцируя (11.20) по безразмерной ординате x = z/h и приравнивая полученное выражение нулю, находим ординату x * нейтральной линии тока. Вычисленные значения безразмерной ординаты нейтральной линии тока x *= d/h как функции параметров a = а/h и b = b/h приведены в табл. 11.3 и представлены графиками на рис. 11.8. Отыскав таким образом ординату нейтральной линии тока x *, по известным методикам можно рассчитать предельный безводный (для нижней части пласта) и предельный безгазовый (для верхней части пласта) дебиты, а затем предельную депрессию. Наименьший дебит из расчетных принимается как предельный безводный и безгазовый дебит скважины.
Рис.11.7. Схема одновременного существования конусов газа и
|

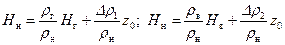 . (11.11)
. (11.11)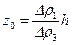 . (11.12)
. (11.12) . (11.13)
. (11.13) . (11.14)
. (11.14) ;
;  , (11.15)
, (11.15)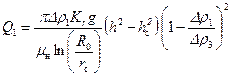 . (11.16)
. (11.16) (11.17)
(11.17)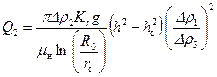 . (11.18)
. (11.18)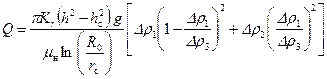 . (11.19)
. (11.19)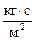 ; [ Q ]=м3/с.
; [ Q ]=м3/с.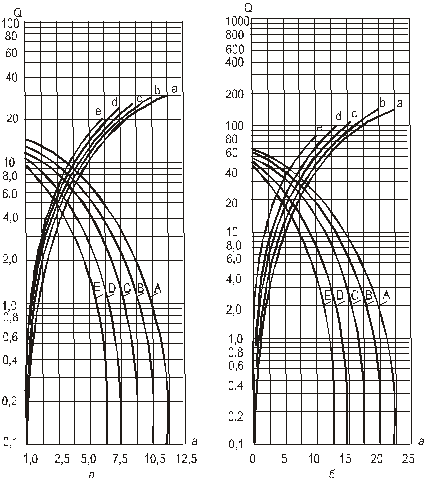

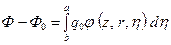 , (11.20)
, (11.20)