Зависимости от расположения интервала вскрытия пласта
Безразмерные предельные дебиты
Очевидно, этот дебит в общем случае является предельным либо для конуса воды (и меньше предельного для конуса газа), либо для конуса газа (и меньше предельного для конуса воды). Выражения в правых частях формул (11.23)
представляют собой соответственно безразмерные предельные безгазовые и безводные плотности расходов. С учетом (11.25) и (11.26) формулы (11.23) принимают вид:
Для каждой пары значений a и b и соответствующих им значений ординат нейтральной линии тока (см. табл. 11.3) по формулам (11.22) подсчитаны величины относительных вскрытий При конкретных расчетах предельных безводных и безгазовых дебитов поступают следующим образом. По известным параметрам a, b и r 0 из таблицы или графиков находят плотности расходов q 1 и q 2, затем по формулам (11.27) подсчитывают удельные расходы q 01 и q 02, из которых выбирают наименьшее значение q 0=min{ q 01; q 02}, и по формуле (11.24) подсчитывают искомый предельный дебит. Покажем применение метода на конкретных примерах. Пример 2. Имеется подгазовая нефтяная залежь, подстилающаяся подошвенной водой. Исходные параметры: R 0=200 м; h =25 м; Dr 1=870 кг/м3; Dr 2=200 кг/м3 (в пластовых условиях); m н=2,5 мПа×с; К r=0,5×1,02×10—12 м2; Dr 2=200 кг/м3 (в пластовых условиях); m н=2,5 мПа×с; Kr =0,5×1,02×10—12 м2; æ;*=12. Требуется определить безводный и безгазовый дебит при безразмерных параметрах вскрытия: a =0,2; b =0,7 и a =0,2; b =0,5. 1. Определяем значение r 0= R 0/ æ;* h =0,66. 2. Из табл. (Прил. 3) находим плотности q 1=0,145 и q 2=0,290 при a =0,2 и b =0,7. 3. По формулам (11.27) находим удельные расходы: q 01=0,145×870 eh =126,15 eh; q 02=0,290×200 eh =58 eh. 4. Так как q 02< q 01, то выбираем q 02. По формуле (11.24) определяем Q =19,4 м3/сут. 5. Из табл. (Прил. 3) при a =0,2 и b =0,5 находим плотности q 1=0,165 и q 2=1,0. 6. Удельные расходы составят соответственно: q 01=0,165×870 eh =143,55 eh; q 02=1.0×200 eh =200 eh. 7. В этом случае принимаем q 01=143,55 eh. Тогда расход по формуле (11.24) составит Q»29,2 м3/сут. Как видим, в этом случае предельный дебит оказался в 1,5 раза больше предыдущего. Таким образом, наибольший дебит зависит от положения интервала вскрытия. Пример 3. Исходные параметры принимаются для Примера 1, интервал вскрытия, в котором определяемый ординатами b =14,84 м и а =2,34 м, соответствуют безразмерным ординатам: b = b / h =14,84/25»0,60 и a = а / h =2,34/25»0,1. 1. По табл. (Прил. 3) для параметров a»0,1, b»0,60 и r 0=200/25=8 при æ;*=1 определяем плотности q 1»0,02, и q 2»0,19. 2. По формулам (11.27) находим удельные расходы: q 01=0,02×870 eh =17,4 eh; q 02=0,19×200 eh =38 eh. 3. Выбираем наименьшую плотность q 01. По формуле (11.23) находим предельный дебит Q =5,9 м3/сут. Сравнивая его значение с дебитом Q =9,87 м3 / сут., рассчитанное по приближенной методике (см. Пример 1), видим, что последний завышает в данном конкретном примере предельный дебит в 1,66 раза. 4. Для сравнения произведем расчет предельного дебита при тех же исходных данных по методике Курбанова-Садчикова, для чего пересчитаем параметры в обозначениях авторов [20]. Получаем: Dr 1/ Dr 2=870/200=4.35; По графикам [20] находим q»0,47 и
Завышение предельного дебита по сравнению с расчетным, учитывающим нейтральную линию тока, в данном случае составляет в 1,72 раза. Пример 4. Принимаются исходные данные, для которых построены графические зависимости размерного предельного безводного и безгазового дебита, рассчитанные потенциометрическим методом [19] и приведенные на рис.14.6д: R 0=1000 футов»305 м; h =100 футов»30.5 м; Dr 1=500 кг/м3; Dr 2=300 кг/м3; Kr =1 д=1 мкм2; m н=1 мПа×с и æ;*=1. Если принять интервал вскрытия l =20 футов»6,1 м, то по графику рис. 14.6д точка пересечения кривых В и b дает Q пр=750 барелей/сут»119 м3/сут и местоположение интервала перфорации а»30 футов»9,15 м (см. рис. 11.7). Следовательно, b = l + а =15,25 м или в безразмерном виде a =0,3 и b =0,5. Параметр r 0= R 0/ æ;* h =10. Определим Q пр по уточненному методу. По табл. (Прил. 3) находим плотности расходов q 1(a, b, r 0)= q 1(0,3;0,5;10)»0,18 и q 2(a, b, r 0)= q 2(0,3;0,5;10)»0,45. Затем, по формулам (11.27) определяем удельные расходы: q 01=0,18×600 eh =108 eh и q 02=0,45×300 eh =135 eh. Для наименьшего удельного расхода q 02 по формуле (11.24) находим Q пр»109 м3/сут. В данном случае расхождение между двумя методами несущественное и составляет 8,4%. Пример 5. За исходные примем данные в примере Курбанова-Садчикова [20]: R 0=200 м; h =10 м; Dr 1=700 кг/м3; Dr 2=300 кг/м3; m н=2 мПа×с; Kr =0,5×1,02×10-12 м2; æ;*=5; b – a =2 м; d =3,9 м (см. рис. 11.7). Из условия задачи имеем численные значения параметров a»0,3 и b»0,5 и r 0=4. По табл. (Прил. 3) определяем безразмерные плотности расходов: q 1»0,213 и q 2»0,557. Удельные расходы составляют: q 01»0,149e h и q 02»0,167 eh. Подсчитывая предельный дебит по формуле (11.24) по наименьшему удельному расходу q 01, получаем Q»6,1 м3/сут. По расчетам авторов [20, 21] этот дебит равен Q»4,33 м3/сут., т.е. отклонение составляет порядка 40%. такое расхождение, очевидно, объясняется тем, что авторы при решении задачи делают допущение, что нейтральная линия тока проходит через середину интервала вскрытия (см. рис. 11.7 и 11.9) при любом его положении, тогда как уточненная методика определяет положение нейтральной линии тока x * в зависимости от положения интервала вскрытия a и b. Заметим, что в своей предпосылке при решении задачи несовершенная скважина считалась линией стоков с постоянным удельным расходом. В действительности на скважине должен быть постоянным потенциал. Физически ясно, что картины линий тока будут отличаться несущественно, а, следовательно, положения горизонтальных линий тока будут близки друг к другу [9]. Метод Курбанова-Садчикова и предлагаемый уточненный метод решения задачи конусообразования имеют следующие преимущества перед потенциометрическим и другими существующими методами: они универсальные, т. е. расчетные зависимости представлены в безразмерном виде и применимы как для однородных, так и для однородно-анизотропных пластов; графические решения даны в широком диапазоне безразмерных параметров вскрытия (a, b) и радиуса контура питания (R 0) и охватывают все практически интересные случаи; технически удобны и просты, не требуют сложной вычислительной техники.
11.3.5. Методика расчета предельной депрессии, обеспечивающей предельный безводный и безгазовый дебит. При вскрытии нефтяной оторочки в интервале (b – a) средние значения потенциала (давления) для каждой части пласта (см. рис. 11.7) будут равными. Вдоль всей вскрытой продуктивной толщи среднее значение потенциала можно определить по формуле
где
Выразим разность потенциалов для каждой из частей пласта, принимая в качестве расхода предельные дебиты:
где в соответствии с формулами (11.27) имеем
Здесь q 1 и q 2 – безразмерные плотности расхода, рассчитанные по формулам (11.25) и (11.26) и затабулированные (см. табл. Прил. 3). С учетом (11.30) и (11.2) имеем
Внося (11.32) и (11.33) в формулу (11.29), переходя к давлению и учитывая (11.31), получаем формулу для предельной депрессии D Р пр= Р 0– Р с в следующем виде:
где Пример 6. Рассчитать предельную депрессию для исходных данных Примера 2 при параметрах вскрытия a =0,2 и b =0,5. 1. По табл. 11.3 определяем ординату нейтральной линии тока: 2. По формулам (11.22) находим: 3. По таблице (11.2) определяем значение функции: 4. Так как 5. Подсчитываем D Р пр по формуле (11.34): D Р пр»0,243 МПа Предельная депрессия может быть подсчитана более точно, если учесть добавочные фильтрационные сопротивления, обусловленные не только частичным вскрытием С 1, но и нарушением линейного закона С 2 и перфорацией колонны С 0. Тогда определяя разность потенциалов по формулам (11.32) и (11.33) с учетом (11.4) и (11.22) для каждой части пласта и внося их выражения в формулу (11.29), после ряда преобразований получаем:
´ где
С 1, С 2, С 0 — добавочные фильтрационные сопротивления в формулах (11.36) определяются по соответствующим формулам или таблицам [10, 12, 18, 28], приведенным в Гл.9 и Прил.1. Пример 7. Применяются исходные данные Примера 6. Добавочные данные: фильтрация происходит по закону Дарси (С 2=0); скважина перфорирована с плотностью m =3 отв/пог. м, глубина пулевого канала l 0=0,3456 м, диаметр пулевого канала 2 r =0,0127 м. Требуется определить предельную депрессию. 1. По формулам (11.37) находим: 2. По формуле (9.5.6) находим: С 01=60,07; С 02=6,00. 3. По формуле (11.36) находим: S 1=67,92; S 2=24.13. 4. По формуле (11.35) имеем D Р пр=0,653 МПа. Как видим, предельная депрессия с учетом добавочных фильтрационных сопротивлений, обусловленных перфорацией, оказалась больше в 0,653/0,243»2,7 раза. Следует заметить, что при известных условиях (большой диаметр пулевых каналов, большая глубина проникновения и оптимальная плотность перфорации) значения С 01 и С 02 могут оказаться отрицательными, что влечет к уменьшению расчетных значений D Р пр.
|

 определяются по табл. 11.1. Чтобы дебит был одновременно безводным и безгазовым, необходимо выбрать наименьший расход, т. е. принять q 0=min{ q 01, q 02}. Тогда предельный расход нефти через скважину будет выражаться как
определяются по табл. 11.1. Чтобы дебит был одновременно безводным и безгазовым, необходимо выбрать наименьший расход, т. е. принять q 0=min{ q 01, q 02}. Тогда предельный расход нефти через скважину будет выражаться как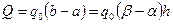 . (11.24)
. (11.24)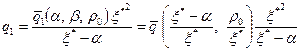 , (11.25)
, (11.25) , (11.26)
, (11.26) . (11.27)
. (11.27)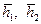 в зависимости от параметров a и b и значения параметров r 01 и r 02.Затем, с помощью таблицы (см. табл. 11.1) для предельных дебитов определялись q 1(a, b, r 0) и q 2(a, b, r 0), а затем по формулам (11.25), (11.26) рассчитывались плотности расходов q 1 и q 2. Результаты расчетов сведены в табл. (Прил. 3), которая охватывает все практически интересные значения параметров a, b и r 0 [16]. В силу симметрии каждая строка таблицы дает одновременно значения безразмерных предельных плотностей расходов q 1 и q 2 для соответствующих значений a и b, т. е. q 1,2(a, b)= q 1,2(1– a, 1– b). По данным таблицы нетрудно построить сетку кривых зависимостей q 1,2= q 1,2(r 0) для фиксированных значений пары параметров a и b, т. е. для заданного интервала вскрытия (b – a).
в зависимости от параметров a и b и значения параметров r 01 и r 02.Затем, с помощью таблицы (см. табл. 11.1) для предельных дебитов определялись q 1(a, b, r 0) и q 2(a, b, r 0), а затем по формулам (11.25), (11.26) рассчитывались плотности расходов q 1 и q 2. Результаты расчетов сведены в табл. (Прил. 3), которая охватывает все практически интересные значения параметров a, b и r 0 [16]. В силу симметрии каждая строка таблицы дает одновременно значения безразмерных предельных плотностей расходов q 1 и q 2 для соответствующих значений a и b, т. е. q 1,2(a, b)= q 1,2(1– a, 1– b). По данным таблицы нетрудно построить сетку кривых зависимостей q 1,2= q 1,2(r 0) для фиксированных значений пары параметров a и b, т. е. для заданного интервала вскрытия (b – a). ;
;  .
. или h»0,095×25»2,38 м. Предельный дебит по формуле [20] составляет
или h»0,095×25»2,38 м. Предельный дебит по формуле [20] составляет .
.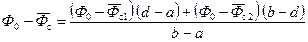 , (11.28)
, (11.28)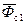 ,
, 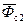 – средние значения потенциалов вдоль скважины по вскрытым толщинам (d – a) и (b – d) соответственно (см. рис. 11.7). В безразмерных параметрах формула (11.28) представляется в виде
– средние значения потенциалов вдоль скважины по вскрытым толщинам (d – a) и (b – d) соответственно (см. рис. 11.7). В безразмерных параметрах формула (11.28) представляется в виде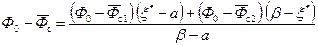 . (11.29)
. (11.29)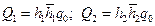 , (11.30)
, (11.30) . (11.31)
. (11.31) ; (11.32)
; (11.32)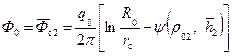 . (11.33)
. (11.33)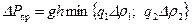 ´
´ (11.34)
(11.34) ,
, 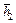 , r 1, r 2 подсчитываются по формулам (11.22). Функция
, r 1, r 2 подсчитываются по формулам (11.22). Функция  затабулирована (см. табл. 11.2).
затабулирована (см. табл. 11.2).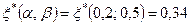 .
.
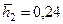 .
.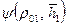 =
= 
 =
=  .
. (см. Пример 2), следовательно,
(см. Пример 2), следовательно, 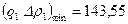 .
.
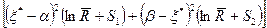 , (11.35)
, (11.35)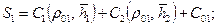
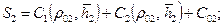 (11.36)
(11.36) . (11.37)
. (11.37) »7,84;
»7,84; 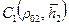 »18,13.
»18,13.


