Упрощенные и строгие методы расчета времени безводной эксплуатации скважин с подошвенной водой
Наиболее простой метод основан на рассмотрении простейшей гидродинамической модели – одножидкостной системы или так называемой модели «разноцветных жидкостей». Она характеризуется тем, что не учитывает различие фильтрационных и физических характеристик вытесняющей и вытесняемой жидкостей, которые могли бы повлиять на динамику конуса. В частности, считается, что соотношение «проницаемость-вязкость» (коэффициент подвижности) для нефти, залегающей над поверхностью раздела вода-нефть, равно такому же соотношению для воды в заводненной части нефтяной зоны. В реальных условиях это не выполняется, поэтому, если коэффициент подвижности для заводненной части будет меньше, чем для нефтенасыщенной, то прорыв конуса произойдет за время, меньшее, чем вычисленное, в противном случае обводнение наступит позднее. Наиболее серьезным допущением является пренебрежение разностью в плотностях между водой и нефтью, но оно сильно облегчает решение, так как делает процесс образования конуса зависящим лишь от геометрических и физических постоянных одножидкостной системы (обычно за них принимают характеристики вытесняемой жидкости – нефти) и независящим от дебитов, которые влияют лишь на масштаб времени. В реальных условиях повышенная плотность воды по сравнению с нефтью приводит к заторможиванию деформации границы раздела и «выпрямлению» конусообразной поверхности вода-нефть. Этот эффект будет проявлять себя лишь при малых отборах нефти и низких эксплуатационных перепадах давления. Полученное П.Б. Садчиковым решение для одножидкостной системы справедливо для следующих условий: пласт бесконечный, нефтенасыщенный слой вскрыт скважиной-стоком с равномерным распределением по длине расходом Q на глубину b; водонасыщенная толщина бесконечна; пласт с пористостью т считается однородно-анизотропным и характеризуется коэффициентом анизотропии æ;*. Так как проницаемость в вертикальном направлении K z связана с геометрическим распределением отдельных и локализованных непроницаемых элементов, залегающих в общей массе пористой среды, анализ керна не может служить для определения ее величины. Формула П.В. Садчикова для расчета безразмерного времени безводной эксплуатации t имеет вид [27].
Приближенная формула Данилова-Салехова для этого случая имеет вид [24]:
Анализ показывает, что формулы (12.1) и (12.2) дают результаты с наибольшим расхождением при наибольшем вскрытии В.Л. Данилов и Р.М. Кац для тех же условий предлагают формулу, которая для безразмерного времени имеет вид [37].
Графические зависимости t = f (
Рис. 12.1. Зависимость времени безводной эксплуатации несовершенной скважины t от относительного вскрытия пласта 1 – по формуле Садчикова (12.1); 2 – по формуле Данилова-Каца (12.3); 3 – по формуле Маскета (12.4) при α;=0,65 и β;=1,3; 4 – по формуле Данилова-Каца [37] при m н=2.3 мПаЧс, m в=1,1 мПаЧс и K =0,6 мкм2; 5 – по формуле Маскета (12.4) α;=1 и β;=1
Время прорыва подошвенной воды можно рассчитать, используя также формулу Маскета [38]:
где a – коэффициент водонасыщенности в зоне вытеснения нефти водой; b – объемный коэффициент пластовой нефти;
Графическая зависимость Заметим, что использование формул (12.3) и (12.4) не может дать приемлемого решения для определения действительного безводного периода, т. к. формула (12.3) получена для бесконечного пласта, а формула (12.4) – для ограниченного. На точность определения параметра t м по формуле (12.3) существенно влияет достоверность параметров т, a, b, а также функции Определив параметр æ;* из формулы (12.4) и подставив в формулу (12.1), получаем выражение для расчетного времени Т безводного периода
из которого видно, что расчетное время будет соответствовать фактическому T ф при выполнении условия
Решая совместно (12.1), (12.5) и (12.4), получаем формулу для определения анизотропии пласта
где t – определяется формулой (12.3). Таким образом, определив æ;* по промысловым данным фактического периода эксплуатации, прогнозирование далее можно вести по формуле (12.1). Для получения наиболее точных результатов необходимо учитывать различие в вязкостях и плотностях вытесняемой и вытесняющей жидкостей. Ю.А. Абрамов и Р.М. Кац [37, 39] предлагают формулу для расчета времени прорыва подошвенной воды с учетом различия в вязкостях вытесняемой m 1 и m 2 вытесняющей жидкостей. Задача решалась для продуктивного пласта бесконечной протяженности и бесконечной водонасыщенной толщины h 0, вскрытого на глубину b Ј h 0 несовершенной скважиной с равномерно распределенным дебитом Q. Для определения времени прорыва конуса подошвенной воды получена сложная формула, требующая использования ЭВМ:
где
Ряд (12.8) сходится на всем интервале Результаты расчета безразмерного времени для условий Туймазинского месторождения при m н=2,3 мПаЧс, m в=1,1 мПаЧс и K =0,6 мкм2 представлены графически кривой 4 на рис. 12.1. Так как формула (12.3) получена из (12.7) при l =0, т. е. для одножидкостной системы, то можно сделать вывод, что учет различия в вязкостях нефти и воды приводит к получению меньшего расчетного времени прорыва подошвенной воды, чем для одножидкостной системы. Это связано с тем, что коэффициент подвижности воды больше, чем нефти. Можно оценить погрешность в определении безразмерного времени, связанную с пренебрежением различия в вязкостях воды и нефти, путем сравнения формул (12.3) и (12.7) из соотношения
Если учесть, что эта погрешность характеризует влияние различия в вязкостях нефти и воды на время прорыва конуса, то можно оценить величину оптимального относительного вскрытия с точки зрения минимального влияния в вязкостях эффективности воды на время безводной эксплуатации по графической зависимости Все приведенные выше формулы для расчета времени безводной эксплуатации получены при условии, что водонасыщенная толщина бесконечна. Из решения задачи для пласта ограниченной водонасыщенной толщины с непроницаемой подошвой в работе [37] делаются следующие выводы:
– при возрастании водонасыщенной толщины, т. е. с удалением подошвы от начального зеркала подошвенной воды, относительное увеличение безводного периода уменьшается; при этом, если водонасыщенная толщина превышает продуктивную более чем в два раза, то влиянием непроницаемой подошвы на движение границы раздела можно пренебречь. В итоге можно сделать вывод, что использование конкретных методов расчета времени безводной эксплуатации будет определяться целью расчетов. В частности, если необходимо лишь оценить время безводной эксплуатации, то можно использовать методы, основанные на рассмотрении одножидкостной системы Формула М. Маскета применима лишь для r 0>0,35. Кроме того, величину a за безводный период можно принять ориентировочно. Формула Абрамова-Каца (12.7), учитывающая различие в вязкостях, дает более точные результаты по сравнению с методами для одножидкостной системы. Практическое применение этой формулы целесообразно, когда соотношение вязкостей нефти и воды достаточно велико. На основании формул, предложенных Абрамовым-Кацем, можно оценить величину оптимального относительного вскрытия пласта с точки зрения минимального влияния различия в вязкостях нефти и воды. Расхождение расчетных и фактических данных во многих случаях объясняется наличием в формулах коэффициента анизотропии æ;*, для определения величины которого не существует универсального метода, поэтому делается лишь приближенная оценка этого важного параметра.
|

 . (12.1)
. (12.1)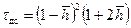 . (12.2)
. (12.2) . Так, при
. Так, при 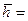 0,9 получаем t дс=1,5 t с.
0,9 получаем t дс=1,5 t с.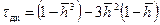 . (12.3)
. (12.3)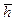 ) представлены на рис. 12.1. Из анализа зависимостей видно, что формула Садчикова (кривая 1) дает заниженные результаты по сравнению с формулой Данилова-Каца (кривая 2) и, с увеличением относительного вскрытия, отличие в результатах может достигать 1,5 раза (например, при
) представлены на рис. 12.1. Из анализа зависимостей видно, что формула Садчикова (кривая 1) дает заниженные результаты по сравнению с формулой Данилова-Каца (кривая 2) и, с увеличением относительного вскрытия, отличие в результатах может достигать 1,5 раза (например, при 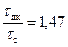 ). Как видно из графика, кривая 4 дает идеальное описание промысловых результатов æ;* определялось по промысловым данным, используя формулу (12.6)].
). Как видно из графика, кривая 4 дает идеальное описание промысловых результатов æ;* определялось по промысловым данным, используя формулу (12.6)].

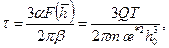 (12.4)
(12.4)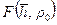 – функция, зависящая от относительной глубины вскрытия нефтенасыщенной части пласта
– функция, зависящая от относительной глубины вскрытия нефтенасыщенной части пласта  (см. фиг. 154 [38]).
(см. фиг. 154 [38]).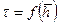 , рассчитанная по формуле (12.4) для предельных параметров a =1 (поршневое вытеснение) и b =1, представлена кривой 5 (см. рис. 12.1). Эта же зависимость представлена кривой 3 на том же рисунке с учетом неполноты вытеснения a =0,65 и объемного коэффициента b =1,3. Как видим, кривая 2 лежит выше предельной кривой 5 (по Маскету), т. е формула Маскета даже для предельных параметров занижает значения безразмерного безводного времени эксплуатации против значений по формуле (12.2). Таким образом, формула Данилова-Салехова дает лишь приближенную оценку времени прорыва подошвенной воды, которая будет характеризовать, в случае, если в пласте нет плохо проницаемых пропластков, максимально завышенное время безводной добычи при данных условиях эксплуатации. Действительные значения t должны лежать ниже кривой 5, положения которых определяется параметрами a и b.
, рассчитанная по формуле (12.4) для предельных параметров a =1 (поршневое вытеснение) и b =1, представлена кривой 5 (см. рис. 12.1). Эта же зависимость представлена кривой 3 на том же рисунке с учетом неполноты вытеснения a =0,65 и объемного коэффициента b =1,3. Как видим, кривая 2 лежит выше предельной кривой 5 (по Маскету), т. е формула Маскета даже для предельных параметров занижает значения безразмерного безводного времени эксплуатации против значений по формуле (12.2). Таким образом, формула Данилова-Салехова дает лишь приближенную оценку времени прорыва подошвенной воды, которая будет характеризовать, в случае, если в пласте нет плохо проницаемых пропластков, максимально завышенное время безводной добычи при данных условиях эксплуатации. Действительные значения t должны лежать ниже кривой 5, положения которых определяется параметрами a и b. (R 0 – половина расстояния между скважинами). В общем случае функция
(R 0 – половина расстояния между скважинами). В общем случае функция  зависит от параметров
зависит от параметров 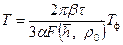 ,
,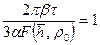 или
или  . (12.5)
. (12.5) , (12.6)
, (12.6) , (12.7)
, (12.7)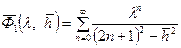 ; (12.8)
; (12.8) (12.9)
(12.9) (12.10)
(12.10) и для практических расчетов достаточно удержать не более пяти членов. Характер сходимости определяется величиной
и для практических расчетов достаточно удержать не более пяти членов. Характер сходимости определяется величиной  .
.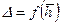 . В частности, для Туймазинского месторождения величина оптимального относительного вскрытия лежит в пределах 0,35
. В частности, для Туймазинского месторождения величина оптимального относительного вскрытия лежит в пределах 0,35 
 наличие подошвы замедляет продвижение границы раздела к скважине; наиболее сильно это влияние проявляется, когда водонасыщенная толщина меньше продуктивной;
наличие подошвы замедляет продвижение границы раздела к скважине; наиболее сильно это влияние проявляется, когда водонасыщенная толщина меньше продуктивной;


