Расчет предельных безводных дебитов несовершенных сважин и депрессий в газовых залежах с подошвенной водой при линейном законе фильтрации
Движение газа предполагается установившимся, изотермическим и следующим закону Дарси. При эксплуатации залежи, вследствие неравномерного распределения давления на поверхности раздела газ-вода, образуются конуса подошвенной воды ниже забоя скважин (см. рис. 11.2). Возникает интересная для газопромысловой практики задача определения предельных безводных дебитов газа и предельных депрессий, при превышении которых в скважины прорывается подошвенная вода. Такая же необходимость в определении предельных безводных дебитов газа возникает и при эксплуатации подземных хранилищ газа в водоносных пластах при наличии подошвенной воды. Если принять основное допущение приближенной теории устойчивых конусов [2], то расчет верхнего значения предельного безводного дебита можно выполнить, используя решение задачи о напорном притоке газа к несовершенной скважине. В такой постановке исследование этой задачи было выполнено Б.Б. Лапуком и С.Н. Кружковым [29] на основе приближенного решения Маскета [1] для притока жидкости к несовершенной скважине. При этом показано, что предельный безводный дебит газа, в отличие от предельного безводного дебита нефти, является функцией трех параметров r, Здесь рассматривается, та же задача, основанная на более эффективном решении 1.3 (17) [9] о напорном притоке к несовершенной скважине по линейному закону в широком диапазоне параметра r и не требующая дополнительного графического построения в отличие от [29]. Задача сводится к решению для притока несжимаемой жидкости с некоторым поправочным коэффициентом δ;, что позволяет использовать уже имеющиеся графики для расчета предельных безводных дебитов. Дается также и оценка коэффициента δ;. Используем решение 1.3 (17) [9], которое для притока газа принимает вид
где Р 0 – средневзвешенное начальное давление. Условие установившегося безводного притока газа, когда водяной конус неподвижен, определяется из закона Паскаля
Пусть предельная высота конуса воды определяется ординатой x=x 0. Тогда, решая совместно (11.38) и (11.39), после некоторых преобразований получаем безразмерный предельный дебит для газовой скважины
Сравнивая формулы (11.40) и (11.1), находим:
Формула (11.43) представляет безразмерный предельный безводный дебит по нефти. Таким образом отпадает необходимость находить x 0 и соответствующую ей функцию
При достаточно большом значении
Выражение для размерного дебита где
При достаточно большом значении Итак, рассчитать предельный безводный дебит газа для газовой залежи можно по безразмерным графикам для предельного дебита нефти (см. табл. 11.1 и рис. 11.3). Из этой же таблицы определяются x 0 и Представляется интересным оценить погрешность формулы (11.45) или (11.48). Нетрудно видеть, что их погрешность оценивается соотношением
Покажем минимальную и максимальную погрешность этих формул. За минимальную погрешность примем d % при r 0=0,05 и
Таблица 11.4
Результаты расчетов погрешности d 0 по формуле (11.49)
Как видно из таблицы для малых значений r 0 и больших значений вскрытия h погрешность формул (11.45) и (11.48) незначительна (первая строка), тогда как с уменьшением вскрытия В работе [29] при определении депрессии исходим из двучленной формулы притока
где Q=Q пр – предельный безводный дебит газовой скважины, который авторами [29] определялся при линейном законе фильтрации. Здесь мы покажем способ определения ΔР пр при линейном законе фильтрации (В =0), который не требует определения предельного расхода Q пр. Из уравнения (11.50) при В =0 следует
где А – коэффициент фильтрационного сопротивления, определяемый как по результатм исследования скважин, так и аналитически (см. §9.2.3)
S = С 1+ С 0+ С ск – суммарные добавочные фильтрационные сопротивления, обусловленные соответственно относительным вскрытием пласта, перфорацией колонны и скин-эффектом. Внося выражение (11.46) в (11.51), получаем
Произведение параметров АQ 0 в соответствии с формулами (11.52) и (11.41) составит:
Вводя безразмерные параметры
и внося (11.54) в (11.53), после ряда преобразований находим выражение для безразмерной депрессии
где
Размерная депрессия определится из соотношения (11.55): Таким образом, для определения ΔР пр необходимо знать средневзвешенное пластовое давление Р 0, плотности ρ;в и ρ;г, геометрию пласта, безразмерный предельный дебит по жидкости q ж, а также безразмерную ординату
|

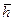 и
и 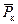 и решение дается графическое в виде семейства кривых для фиксированных значений параметра ρ;0>1 Расчеты могут быть произведены по формулам и графикам для несжимаемой жидкости с погрешностью не более 10% [29].
и решение дается графическое в виде семейства кривых для фиксированных значений параметра ρ;0>1 Расчеты могут быть произведены по формулам и графикам для несжимаемой жидкости с погрешностью не более 10% [29].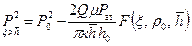 , (11.38)
, (11.38)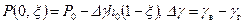 . (11.39)
. (11.39)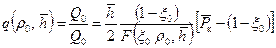 ; (11.40)
; (11.40)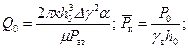
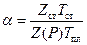 (11.41)
(11.41)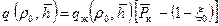 ; (11.42)
; (11.42)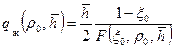 . (11.43)
. (11.43)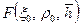 в формуле (11.40), связанную с распределением потенциала в пласте, т. к. они уже рассчитаны для притока несжимаемой жидкости (см табл. 11.1, рис. 11.3). А потому определение безводных дебитов в газовых залежах не представляет принципиальных трудностей. Формулу (11.42) можно записать в виде
в формуле (11.40), связанную с распределением потенциала в пласте, т. к. они уже рассчитаны для притока несжимаемой жидкости (см табл. 11.1, рис. 11.3). А потому определение безводных дебитов в газовых залежах не представляет принципиальных трудностей. Формулу (11.42) можно записать в виде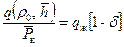 . (11.44)
. (11.44)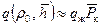 (11.45)
(11.45)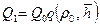 с учетом (11.41) и (11.44) запишется формулой
с учетом (11.41) и (11.44) запишется формулой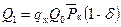 , (11.46)
, (11.46)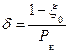 (11.47)
(11.47)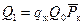 . (11.48)
. (11.48)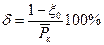 (11.49)
(11.49)
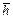 =0,8; x 0=0,97
r 0=1;
=0,8; x 0=0,97
r 0=1; 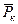 ³8 погрешность формул (11.45) и (11.48), даже для больших значений r 0, не превосходит 10%. Заметим, что в работе [29] оценивается погрешность d <10% при
³8 погрешность формул (11.45) и (11.48), даже для больших значений r 0, не превосходит 10%. Заметим, что в работе [29] оценивается погрешность d <10% при 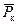 >10.
>10.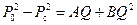 , (11.50)
, (11.50)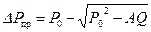 , (11.51)
, (11.51)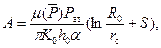 (11.52)
(11.52) (11.53)
(11.53)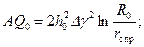
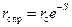 . (11.54)
. (11.54)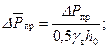
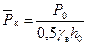 (11.55)
(11.55)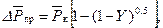 (11.56)
(11.56)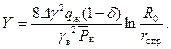 (11.57)
(11.57)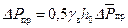 .
.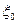 вершины конуса, метод определения которых изложен в § 11.2.2.
вершины конуса, метод определения которых изложен в § 11.2.2.


