Методика прогнозирования продвижения границы раздела и нефтеотдачи за безводный период по удельному объему дренирования
При проектировании и разработке водонефтяных и газонефтяных зон месторождений встают такие практические задачи, как определение и прогнозирование предельных безводных и безгазовых дебитов и депрессий, безводного и безгазового периодов эксплуатации и безводной (безгазовой) нефтеотдачи, соотношения дебитов нефти и воды, газа и нефти при совместном притоке к несовершенной скважине, времени истощения залежи и конечного коэффициента нефтеотдачи и газоотдачи. Аналогичные задачи возникают и при разработке газовых залежей с подошвенной водой. Некоторые из этих вопросов рассматривались и широко обсуждались в печати, однако указанная проблема далека от завершения и требует дополнительных исследований с целью создания рабочей инженерной методики по определению основных показателей разработки водонефтяных, газонефтяных и водогазовых зон. Разработка трещиноватого коллектора несовершенными скважинами при наличии подошвенной воды сопровождается более интенсивным прорывом последней к забою скважины из-за высокой проницаемости по вертикальным трещинам по сравнению с продвижением конуса воды в обычных породах-коллекторах. Естественно возникает вопрос об изоляции подошвенных вод, методы которых широко освещены в литературе. При этом эффективность изоляционных работ будет зависеть от глубины проникновения изолирующего агента, который должен быть дешевым и легко доступным. Прежде всего требуются дополнительные исследования динамических задач конусообразования при дебитах и депрессиях выше их предельных значений. Эти задачи относятся к классу задач с подвижной границей и решения их представляются сложными функциями, требующими численного интегрирования с применением ЭВМ. Надо сказать, что число работ, относящихся к пространственным задачам динамики границы двух жидкостей в пористой среде, весьма ограничено [2-4, 14, 15, 21, 32, 34, 35]. Наиболее эффективными в математическом отношении является решения В.Л. Данилова, Р.М. Каца, Ю.С. Абрамова [23, 37, 39] для несовершенной линии-стока по степени вскрытия однородного полубесконечного пласта (рис. 12.2) с равномерно распределенной плотностью расхода, учитывающие различие в вязкостях жидкостей в условиях поршневого вытеснения. Авторы вывели очень сложные для вычислений интегродифференциальные уравнения движения границы раздела в безразмерных переменных [37, уравнение (IV.2.53), стр. 133], не получившие своей реализации. Опуская в уравнении параметр А, выражающий отношение гравитационных и динамических сил, авторы приходят к уравнению Фредгольма второго рода, решение которого представляется в виде ряда Неймана по параметру l, учитывающего коэффициенты подвижности нефти и воды при поршневом вытеснении [37, (IV.2.57), стр. 134]. Это решение также не получило реализации из-за трудностей, сопряженных с отысканием последовательных приближений ряда. Авторы ограничились случаем главного направления движения точки границы раздела по оси скважины (r =0) и получили приближенную формулу:
где
b – вскрытие пласта; h н – начальная нефтенасыщенная толщина; Q – дебит скважины; т – коэффициент пористости; t – время продвижения точки по оси скважины, определяющее ординату вершины конуса z 0; Ki, mi – коэффициенты проницаемости и вязкости (i =1, 2 – соответственно для нефти и воды).
Рис. 12.2. Схема продвижения границы раздела нефть—вода: 1 – при полном обводнении; 2 – при совместном притоке; 3 – в момент прорыва воды; 4 – в безводный период
Функция Т 1 рассчитана на ЭВМ и представлена графиком [37, рис. IV.33, с. 134]. Для «разноцветных» жидкостей (одножидкостная система), то есть при l =0, из формулы (12.11) следует точное решение для движения точки раздела по оси скважины в однородно-анизотропном пласте
при f 0=
Для ограниченной толщины пласта, то есть с учетом толщины водонасыщенной зоны, в работе [37] расчетные формулы не приводятся из-за их громоздкости. Но авторы приводят результаты таких расчетов, из которых видно, что наличие непроницаемой подошвы замедляет продвижение границы раздела к скважине. Наибольшее влияние непроницаемая подошва оказывает, когда водонасыщенная толщина h в меньше продуктивной h н, то есть когда h в/ h н<1. При h в/ h н>2 продолжительность безводного периода уже не зависит от водонасыщенной толщины. В такой же постановке авторы [37] решают пространственную задачу двухфазной фильтрации (продвижение границы раздела к несовершенной линии-стоку до прорыва воды к забою и совместный приток жидкостей) методом конечных разностей, пренебрегая различием плотностей нефти и воды и капиллярным давлением. Полученный алгоритм был реализован для двухфазной аппроксимации области притока с использованием зависимостей: относительных фазовых проницаемостей от насыщенности K 1(s)=(1– s)2; K 2(s)= s 2; s =0,3015 и параметров m 1/ m 2=10, Из приведенного анализа становится ясно, что рассматриваемая задача, столь важная для нефтепромысловой практики, требует дальнейшего своего изучения. Дело в том, что не только надо уметь рассчитывать безводный период, но и оценить удельный объем дренирования, время истощения и конечную нефтеотдачу по возможности с учетом реальных свойств пласта и жидкостей. Такой подход к расчету процесса обводнения некоторых скважин Мегионского, Трехозерного и Мортымья-Тетеревского месторождений был произведен в работе [40], в которой приведено упрощенное решение интегро-дифференциального уравнения, полученного Ю.С. Абрамовым [37, 39], для условий притока «разноцветных» жидкостей (l =0, и А =0) при поршневом вытеснении в однородно-анизотропном пласте:
где
Kr и K z – проницаемость по горизонтали и вертикали соответственно. При
Как видим, формулы (12.16) и (12.19) идентичны.
Таким образом, решая совместно (12.19) и (12.20) при фиксированных значениях При
Решая совместно (12.21) и (12.20) при t 0= t б, определяем радиус пространственного притока Начальные удельные запасы нефти за безводный период в области удельного объема дренирования, ограниченного условным радиусом
Остаточные запасы в необводненной зоне, ограниченной в вертикальном сечении границей раздела f=f (
где значения безразмерных величин
Рис. 12.3. Схема к расчету удельного объема дренирования и нефтеотдачи за безводный период
Суммарное количество добытой и остаточной нефти в объеме конуса за счет неполноты вытеснения определяется формулой
Коэффициент нефтеотдачи за безводный период выразится формулой
При суммировании (12.25) следует принять при п =1 значение Легко видеть, если в формуле (12.18) принять s = s 0 (s 0 – остаточная нефтенасыщенность), то получим количество остаточной нефти V ок в объеме конуса за безводный период. С другой стороны, эта величина определяется разностью где Q – суммарное количество добытой нефти; В – объемный коэффициент нефти. Тогда приравнивая (12.24) при s = s 0 и (12.26), получаем соотношение
Таким образом, по начальной нефтенасыщенности s и суммарному количеству добытой жидкости Q определяется остаточная нефтенасыщенность s 0, а затем по формуле (12.18) при s = s 0 – количество остаточной нефти V ок. По указанной схеме, зная положение границы раздела на момент времени t, можно определить текущую нефтеотдачу и остаточную нефтенасыщенность в заводненном объеме. Рассмотрим неустановившийся совместный приток нефти и воды при дренировании нефтяной оторочки (см. рис. 12.2). Принимая в уравнении (12.18) вместо относительного вскрытия Время истощения залежи (полного обводнения) t 0и определяется из формулы (12.21) при
Подставляя в формулу (12.18) t 0= t 0и= æ;*2 и
Задавая В условиях интерференции скважин при условном контуре питания R к, равным половине расстояния между скважинами, для определения ординаты Принимая отношение дебита воды Q в к дебиту нефти Q н при совместном притоке пропорционально площадям фильтрации фаз на контуре скважины, т. е.
из уравнения (12.18) при
Здесь t определяется по формуле (12.1) при æ;*=1 и Q=Q н. Соотношение (12.31) не учитывает неполноту вытеснения, разность в вязкостях и плотностях жидкостей. Учет фазовых проницаемостей и подвижности жидкостей приводит к прямому решению сложной задачи двухфазной фильтрации методом конечных разностей [37], что затрудняет его широкую реализацию. Здесь предлагается учет указанных параметров косвенным путем. В работе [41] предложена формула, определяющая водонефтяной фактор R в с учетом несовершенства скважины, анизотропии ограниченного пласта, перепада давления, фазовых проницаемостей, различия в вязкостях и плотностях жидкостей в условиях квазиустановившегося притока, которая после некоторых упрощений принимает вид:
где
Решая совместно (12.30) и (12.32), находим
Расчет процесса обводнения предлагается производить по следующей схеме: – приняв для неограниченного пласта – затем строим графическую зависимость Схему для совместного притока нефти и газа при дренировании нефтяной оторочки следует рассматривать в обратном изображении схемы для совместного притока воды и нефти (см. рис. 12.2), в которой все геометрические параметры для водоносного пласта заменить на параметры нефтяного пласта, а параметры нефтяного пласта на параметры газоносного. Приведенные расчетные формулы остаются справедливы и для совместного притока нефти и газа, если в них все физические параметры для воды Предложенная методика справедлива для модели однородно-анизотропного неограниченного по простиранию пласта при достаточно большой водонасыщенной толщине (h ві2 h н). В условиях интерференции скважин при условном контуре питания R к, равном половине расстояния между скважинами, для определения ординаты Анализируя уравнения, таблицы и графические зависимости (см. [42] Прил. 3-8) можно сделать следующие выводы: – радиус зоны пространственного притока – степень выработки и удельный объем дренирования пласта увеличиваются с увеличением анизотропии; – безводный период возрастает с увеличением анизотропии и уменьшением относительного вскрытия пласта. Изложенную здесь методику можно также использовать в расчетах, связанных с продвижением границы раздела нефть-газ (ГНК) при дренировании нефтяной зоны несовершенной скважиной, предварительно заменив в формулах все геометрические и физические параметры, относящиеся к водоносному пласту, на соответствующие параметры нефтеносного пласта. Заметим, что с целью получения наиболее достоверной информации о пласте гидродинамические исследования скважины с подошвенной водой необходимо проводить при дебитах меньше их предельных значений. Учет интерференции несовершенных скважин в залежах с подошвенной водой при расчетах времени безводной эксплуатации подробно рассмотрен нами в работе [31].
|

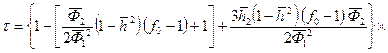
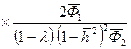 , (12.11)
, (12.11)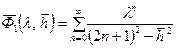 ; (12.12)
; (12.12)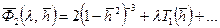 ; (12.13)
; (12.13)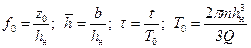 ; (12.14)
; (12.14)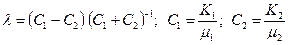 ; (12.15)
; (12.15)
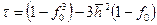 ; (12.16)
; (12.16)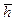 получаем время безводного периода t 0. Для определения времени появления точки возврата (перед прорывом воды в скважину) авторы [37] получили формулу (t < t *)
получаем время безводного периода t 0. Для определения времени появления точки возврата (перед прорывом воды в скважину) авторы [37] получили формулу (t < t *)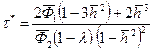 . (12.17)
. (12.17) (12.18)
(12.18)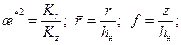
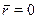 и f = f 0= z 0/ h н из выражения (12.18) следует уравнение движения точки по оси скважины
и f = f 0= z 0/ h н из выражения (12.18) следует уравнение движения точки по оси скважины (12.19)
(12.19) Чтобы получить уравнение движения точки вдоль начального ВНК, надо принять в выражении (12.18) f =1, что приводит t =0. Чтобы избежать этой особенности, примем в формуле (12.18) f =1 под корнем и f =0,99 в числителе. Получаем:
Чтобы получить уравнение движения точки вдоль начального ВНК, надо принять в выражении (12.18) f =1, что приводит t =0. Чтобы избежать этой особенности, примем в формуле (12.18) f =1 под корнем и f =0,99 в числителе. Получаем: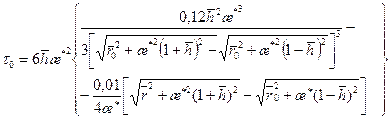 (12.20)
(12.20)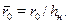 Для построения границы раздела по формуле (12.18) принимаем снова t = t 0, 0<
Для построения границы раздела по формуле (12.18) принимаем снова t = t 0, 0< 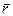 <
< 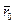 и находим соответствующую ординату f заданному значению
и находим соответствующую ординату f заданному значению 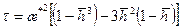 . (12.21)
. (12.21)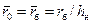 за безводный период; далее при t = t б и 0< r < r б из совместного решения (12.21) и (12.18) находим соответствующие фиксированным значениям
за безводный период; далее при t = t б и 0< r < r б из совместного решения (12.21) и (12.18) находим соответствующие фиксированным значениям 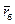 = R у/ h н, определятся, очевидно, по формуле
= R у/ h н, определятся, очевидно, по формуле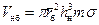 . (12.22)
. (12.22)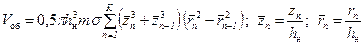 , (12.23)
, (12.23)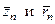 определяются непосредственно из схемы (см. рис. 12.3), которая по возможности должна быть выполнена аккуратно в соответствующем масштабе.
определяются непосредственно из схемы (см. рис. 12.3), которая по возможности должна быть выполнена аккуратно в соответствующем масштабе.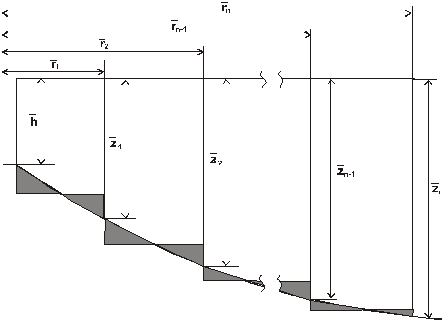
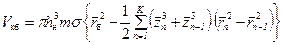 . (12.24)
. (12.24)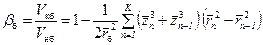 . (12.25)
. (12.25)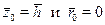 .
.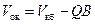 , (12.26)
, (12.26)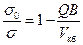 . (12.27)
. (12.27)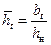 , получим уравнение границы раздела при совместном притоке нефти и воды (см. рис. 12.2, кр. 2). При
, получим уравнение границы раздела при совместном притоке нефти и воды (см. рис. 12.2, кр. 2). При 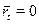 имеем
имеем 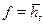 , тогда из формулы (12.18) следует уравнение движения вершины конуса вдоль оси скважины
, тогда из формулы (12.18) следует уравнение движения вершины конуса вдоль оси скважины  , которое выражается формулой (12.21) при
, которое выражается формулой (12.21) при 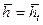 . Принимая в формуле (12.20)
. Принимая в формуле (12.20) 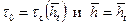 , находим радиус зоны пространственного притока r 0 при совместном притоке нефти и воды. Затем, задавая текущий радиус r 0 в пределах
, находим радиус зоны пространственного притока r 0 при совместном притоке нефти и воды. Затем, задавая текущий радиус r 0 в пределах 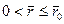 , при
, при 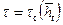 по формуле (12.18) находим соответствующие ординаты f и строим график границы раздела. После чего, по методике, изложенной выше, определяем текущий удельный объем дренирования и коэффициент нефтеотдачи при совместном притоке.
по формуле (12.18) находим соответствующие ординаты f и строим график границы раздела. После чего, по методике, изложенной выше, определяем текущий удельный объем дренирования и коэффициент нефтеотдачи при совместном притоке.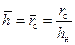 , получаем уравнение для определения радиуса зоны пространственного притока
, получаем уравнение для определения радиуса зоны пространственного притока 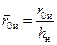 на момент истощения (см. рис. 12.2, кр. 1):
на момент истощения (см. рис. 12.2, кр. 1):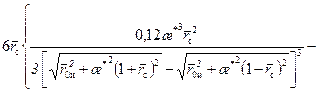
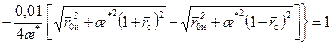 . (12.28)
. (12.28) , получаем уравнение границы на момент истощения удельного объема дренирования:
, получаем уравнение границы на момент истощения удельного объема дренирования: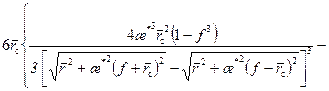
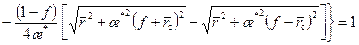 . (12.29)
. (12.29)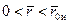 , по формуле (12.29) находим соответствующие значения
, по формуле (12.29) находим соответствующие значения 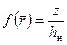 и строим границу раздела в безразмерных координатах. Определение удельного объема дренирования, коэффициента нефтеотдачи и остаточной нефтенасыщенности производим по методике, изложенной выше.
и строим границу раздела в безразмерных координатах. Определение удельного объема дренирования, коэффициента нефтеотдачи и остаточной нефтенасыщенности производим по методике, изложенной выше.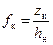 (z к – размерная ордината на контуре питания R к) при
(z к – размерная ордината на контуре питания R к) при 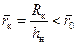 и
и 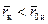 в уравнении (12.18) и (12.19) следует принять
в уравнении (12.18) и (12.19) следует принять 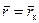 . Таким образом можно определить и скорость подъема ВНК на контуре R к как в безводный период, так и в условиях совместного притока нефти и воды к скважине.
. Таким образом можно определить и скорость подъема ВНК на контуре R к как в безводный период, так и в условиях совместного притока нефти и воды к скважине.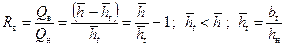 , (12.30)
, (12.30)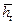 во времени T:
во времени T: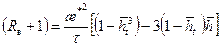 . (12.31)
. (12.31)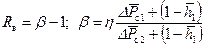 ; (12.32)
; (12.32)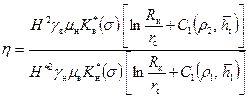 ; (12.33)
; (12.33) 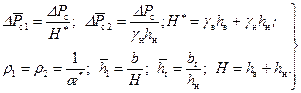 . (12.34)
. (12.34) . (12.35)
. (12.35)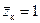 и определив радиус
и определив радиус 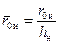 (r 0и — радиус зоны дренирования на момент полного обводнения скважины) по формуле (12.28), при известных исходных данных по формулам (12.1), (12.31) и (12.35) определяем высоту
(r 0и — радиус зоны дренирования на момент полного обводнения скважины) по формуле (12.28), при известных исходных данных по формулам (12.1), (12.31) и (12.35) определяем высоту 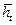 текущего фильтрационного потока на контуре скважины, и водонефтяной фактор R в;
текущего фильтрационного потока на контуре скважины, и водонефтяной фактор R в;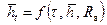 и
и 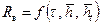 .
.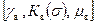 заменить соответственно на параметры для нефти, а водонефтяной фактор R в заменить на газонефтяной фактор
заменить соответственно на параметры для нефти, а водонефтяной фактор R в заменить на газонефтяной фактор 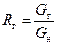 , выраженный через массовые расходы газа (G г) и нефти (G н).
, выраженный через массовые расходы газа (G г) и нефти (G н).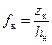 (
(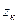 – ордината на контуре R к при
– ордината на контуре R к при 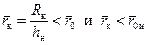 в уравнении (12.18) следует принять
в уравнении (12.18) следует принять 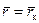 . Формулы (12.21), (12.20), (12.19), (12.28) и (12.29) запрограммированы (фонды кафедры РЭНМ ТюмГНГУ) и рассчитаны: время безводного периода t б; радиус зоны пространственного притока
. Формулы (12.21), (12.20), (12.19), (12.28) и (12.29) запрограммированы (фонды кафедры РЭНМ ТюмГНГУ) и рассчитаны: время безводного периода t б; радиус зоны пространственного притока 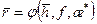 на момент обводнения t 0 и истощения t ис для различных значений вскрытия пласта
на момент обводнения t 0 и истощения t ис для различных значений вскрытия пласта 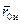 зоны пространственного притока от анизотропии пласта æ;*; зависимости безводного периода t б от æ;* и
зоны пространственного притока от анизотропии пласта æ;*; зависимости безводного периода t б от æ;* и 


