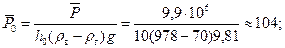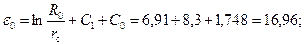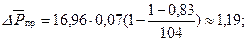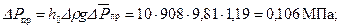Решение задач конусообразования по двухзонной схеме притока
11.5.1. Расчет предельных дебитов несовершенных скважин и депрессий в однородно-анизотропном круговом пласте с подошвенной водой в случае притока вязкопластичной нефти. Методика расчета предельных безводных дебитов для притока неньютонговских нефтей остается такой же, как и для обычных вязких нефтей. Принимая двухзонную схему притока нефти с подошвенной водой (см. рис. 11.2), записывается условие устойчивости для двух точек поверхности раздела жидкостей и вводя коэффициент структурномеханической вязкости нефти η;(τ;0) и ординату
Используя решение IX (47) и IX (48') [12] для притока вязкопластичной нефти к несовершенной скважине, при r =0 получаем [12]:
где
Здесь функция Предельный безразмерный безводный дебит находится из совместного решения уравнений (11.5.2) и (11.5.3) при x=x 0 по формуле:
где
Значение ординаты x 0 можно определить графическим путем из уравнения (11.5.3) или из совместного решения уравнения (11.5.3) и его производной Заметим, формула (11.5.4) имеет такой же вид, как и формула для притока нъютоновской жидкости, только вместо функции Изложим методику определения предельного безводного дебита. Пусть заданы следующие параметры пласта: Находим следующие безразмерные параметры:
При При Здесь Для вязко-пластичной жидкости расчеты будем производить по формулам (11.5.2) и (11.5.3) с использованием табл. 11.1 для определения функции
Рис. 11.9. Графическое решение уравнения (11.5.3). Определение ординаты x 0 и функции Е 0(x 0, r,
Установлено [12], что безразмерные безводные дебиты для притока ненъютоновских жидкостей несколько выше, чем для обычных нефтей. Причем для большинства относительных вскрытий ( Существенно также влияет на величину безразмерного дебита соотношение Несмотря на некоторое увеличение безразмерных предельных дебитов для вязкопластичных нефтей, по сравнению с притоком обычных вязких нефтей, однако нельзя утверждать, что абсолютные (размерные) предельные безводные дебиты для первых жидкостей будут большими. На самом деле, дебит Q определяется из соотношения (11.5.4)как Там, где имеет место течение нефти с разрушенной или ослабленной структурой, вязкости таких нефтей, как правило, превосходят вязкости обычных нефтей в 2-10 раз, что не может никак компенсировать сравнительно малое (25-30%) увеличение безразмерных предельных дебитов[12]. Если предположить, что всюду, от контура питания вплоть до забоя, имеет место течение вязкопластичной жидкости с нарушенной структурой, то потенциал скорости фильтрации, согласно [9], можно выразить, как обычно, Очевидно, большие по величине предельные добиты окажутся в случае очень высокой анизотропии пласта, когда из-за резко ухудшенной проницаемости по вертикали фильтрация нефти преимущественно будет происходить вдоль напластования. Ддя пласта монолитного и более-менее однородно-изотропного картина будет совершенно иная. Ввиду высокой вязкости нефти и однородного строения пласта подвижность подошвенной воды, вязкость которой в десятки и сотни раз может быть меньше вязкопластичной нефти в пластовых условиях, оказывается весьма высокой в вертикальном направлении, чем подвижность нефти в горизонтальном направлении. Поэтому безводный период, а также Предельная депрессия или предельное забойное давление Р смогут быть определены по по соответствующим формулам §11.2, если вместо Q подставить предельный дебит
Здесь
Р ст – восстановленное забойное давление; D Р 0 – давление, расходуемое на преодоление предельного напряжения сдвига (определяется по индикаторным кривым [30];
Учет несовершенства скважины по характеру и нарушение закона Дарси может быть выполнен путем, изложенным в предыдущем параграфе. Расчет давления на устье можно произвести по известным формулам.
11.5.2. Расчет предельных дебитов и депрессий газовых скважин. Чтобыперейти к формулам и уравнениям для фильтрации газа, по известным решениям для притока нефти, согласно М. Маскету [1], необходимо, например, для выражения весового (массового) расхода G заменить депрессию D Р на соотношение Таким образом, устанавливается следующая закономерность: для расчета предельного безводного дебита газовой скважины с подошвенной водой и предельной депрессии могут быть использованы конечные формулы двухжидкостной системы, если в них объемный расход Q вытесняемый жидкости заменить соотношением
где Р ат – давление в поверхностных условиях;
Т ст – температура при стандартных условиях; Т – температура пласта; Z – коэффициент сверхсжимаемости газа; m – параметр, определяющий термодинамический характер расширения газа при фильтрации его из области высокого давления в область пониженного давления. При m =1 происходит изотермическое расширение газа. В случае адиабатического расширения На основании вышеизложенного, формулы, приведенные в §11.2, для газовых скважин преобразуются к следующему виду. Для предельного безводного дебита:
где
r 0 – параметр размещения скважин в условиях их взаимодействия;
æ;* – анизотропия пласта; Kr – проницаемость по горизонтали; Kz – проницаемость по вертикали; r в, r г – плотности воды и газа в пластовых условиях. Для безразмерной предельной депрессии имеем:
где
x 0 – безразмерная ордината вершины конуса (см. рис. 9.2); r с – радиус скважины;
Для x 0 построены графики (см. § 11.2). Возможно другое, наиболее полное представление для функции фильтрационных сопротивлений:
S = C 1+ C 2+ C 0. (11.5.14) где С 1, С 2 и С 0 – добавочные фильтрационные сопротивления, обусловленные различными видами несовершенства скважин и определяемые по соответствующим формулам и графическим зависимостям (см. § 11.2). Более точно величина предельной депрессии определяется из двухчленного закона фильтрации газа:
откуда следует для изотермического процесса формула
Если же известны коэффициенты А и В в двухчленной формуле притока, полученные по данным испытаний скважин, и определен предельный дебит Q газовой скважины, то предельная депрессия определится из формулы
Пример 8. Рассчитать предельные безводные дебиты и депрессии газовой скважины Коимсомольского месторождения, дренироующей сеноманскую залежь при следующих исходных данных: Р пл=9,9 МПа; Р ат=0,1013 МПа; Т пл=301 К; Т ст=293 К; Z ( Решение: – по табл. 11.1 или графикам рис.11.3 определяем для – высота вершины конуса определится из соотношения Y к= h 0(1– ξ;0)=10(1–0,83)=1,7 м; – по формуле (9.2.10) или по таблице (Прил.1) определяем добавочное фильтрационное сопротивление С 1= f (ρ;0, – по формуле (9.5.6) или из графиков рис. 9.17 или рис. 9.18 при исходных данных находим С 0=1,748; – по формуле (11.5.12) определяем безразмерный параметр
– по формуле (11.5.13) определяем фильтрационное сопротивление ε;0.
– по формуле (11.5.11) определяем безразмерную предельную депрессию
Отсюда следует размерная предельная депрессия
– по формуле (11.5.9) рассчитываем Q 0 при исходных данных, принимая m=1; получаем Q 0=2353,1 тыс.м3/сут; следовательно, Q пр= Q 0 q (ρ;0, литература К ГЛ. 11
1. Маскет М. Течение однородных жидкостей в пористой среде (пер. с англ.). – М., Гостоптехиздат, 1949. 2. Чарный И.А. Подземная гидрогазодинамика. – М., Гостоптехиздат, 1963. — 312 с. 3. Чарный И.А. О прорыве подошвенной воды в нефтяную скважину. – ДАН СССР, 1953, т. 91, № 6. – С. 67-91. 4. Чарный И.А. О предельных дебитах и депрессиях в водоплавающих и подгазовых нефтяных месторождениях. – Труды совещания по развитию научно-исследовательских работ в области вторичных методов добычи нефти. – Баку, 1953. – С. 112-115. 5. Чарный И.А. Об одном интегральном соотношении теории фильтрации и его некоторых приложениях. – Материалы межвузовского совещания. Гостоптехиздат, 1958, т. 1. – С. 73-81. 6. Чарный И.А. Приток к скважине в месторождениях с подошвенной водой или газовой шапкой. – Нефтяное хозяйство, 1952, № 10. – С. 11-19. 7. Лапук Б.Б., Брудно А.Л., Сомов Б.Е. О конусах подошвенной воды в газовых залежах. – Газовая промышленность, 1961, № 2. – С. 7-14. 8. Лапук Б.Б., Брудно А.Л., Сомов Б.Е. О конусах подошвенной воды в нефтяных месторождениях. – Нефтяное хозяйство, 1961, № 5. – С. 18-24. 9. Телков А.П., Стклянин Ю.И. Образование конусов воды при добыче нефти и газа. – М., Недра, 1965. – 205 с. 10. Алиев З.С. Разработка и внедрение газогидродинамических методов получения исходной информации и обоснование технологического режима эксплуатации газовых и газоконденсатных месторождений. Докт. диссер., 1984 (фонды МИНХ и ГП им. акад. И.М. Губкина). 11. Эфрос Д.А., Аллахвердиева Р.Г. Расчет предельных безводных и безгазовых дебитов несовершенных скважин по данным исследования. – Тр. ВНИИ, 1957, вып. 10. С. 101-130. 12. Телков А.П. Подземная гидрогазодинамика. – Уфа, Башиздат, 1974. – 224 с. 13. Телков А.П. Некоторые особенности эксплуатации нефтяных залежей с подошвенной водой. – НТО. М., ВНИИОЭНГ, 1972, – 136 с. 14. Телков А.П., Стклянин Ю.И. Расчет предельных безводных и безгазовых дебитов в подгазовых нефтяных залежах с подошвенной водой. – Тр. МИНХ и ГП, 1963, вып. 42. 15. Телков А.П. К вопросам расчета конусов в нефтяных и газовых месторождениях. – Газовая промышленность, 1961, № 5. –С. 12-17. 16. Отчет «Гидродинамические методы расчета, связанные с совместным притоком двух и трех жидкостей к несовершенным скважинам, применительно к нефтегазовой залежи пласта АС Лянторского месторождения» часть I, (А.П. Телков и др.) – 1990. –141. – Фонды НГДУ «Лянторнефть». 17. Интерпретационные модели нефтяной залежи на стадии разработки / А.П. Телков, А.К. Ягофаров, А.У. Шарипов, И.И. Клещенко. – М., ВНИИОЭНГ. – 1993. – 72 с. 18. Телков В.А. Решение задач гидрогазодинамики, связанных с интерпретацией результатов исследования пластов и скважин. – Канд. дис., 1982, 212 с. (Фонды ТюмИИ). 19. Chaney P.G. et. cet. How to Perfate Your well to Prevent Water and. Gas Coning. – J. Oil and Gas. – September, 1971. – Р. 27-35. 20. Курбанов А.К., Садчиков П.Б. Расчет положения интервала вскрытия и предельного дебита скважин в нефтяном пласте с подошвенной водой и газовой шапкой. – Тр. ВНИИ, 1962, вып. 37. С. 29-40. 21. Справочное руководство по проектированию разработки и эксплуатации нефтяных месторождений. – М., Недра, 1983 (под редакцией д.т.н. Ш.К. Гиматудинова). – 702 с. 22. Курбанов А.К., Суворов Н.И. Актуальные вопросы проектирования разработки нефтегазовых залежей. – М., Наука, 19714. – 265 с. 23. Конев В.Д. и др. Выбор рационального расположения интервала перфорации относительно ВНК и ГНК в условиях IV меотического горизонта Анастасиевско-Троицкого месторождения. – Нефтепромысловое дело, ВНИИ, 1967, № 4. – С. 5. 24. Стклянин Ю.И., Телков А.П. Расчет предельных безводных дебитов в однородно-анизотропных пластах с осевой симметрией. – ПМТФ АН СССР, 1961, № 5. – С. 46-514. 25. Телков А.П., Грачев С.И. Особенности разработки нефтегазовых месторождений (4.2). –Тюмень-ООО НИПИКБС-т. –2001. – 482 с. 26. Телкрв А.П. Определение предельного безводного дебита нефти и газа в анизотропных пластах.- "Газовая промышленность".–1962, вып. 8. 27. Телков А. П., Краснова Т.Л. Обоснование технологических режимов работы несовершенных скважин дренирующих нефтегазовые залежи с подошвенной водой /"Геология, геофизика и разработка нефтяных местороэждений"- ВНИИОЭНГ. –1997. – № 4-5. – С. 2-9. 28. Телков А. П., Федорцов В.К. Приток к несовершенной скважине и выбор плотности перфорации.- В кн.: Управление гидродинамическими процессами при разведке и эксплуатации месторождений нефти. – Тр.ЗапСибНИГНИ. – 1986. – С.61-614. 29. Лапук Б.Б., Кружков С.Н. Определение предельного безводного дебита скважин и предельной депрессии в газовых залежах с подошвенной водой. – АНХ, № 3, 1961. 30. Оруджев В.Л., Рахимов Н.Р. Результаты исследованиявязкопла стичных свойств аномальных нефтей Узбекистана. – Нефтяное хозйство, № 10, 1968.
|

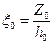 вершины устойчивого конуса воды, получаем
вершины устойчивого конуса воды, получаем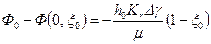 . (11.5.1)
. (11.5.1)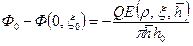 , (11.5.2)
, (11.5.2)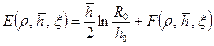 . (11.5.3)
. (11.5.3)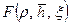 определяется рядом IX (48’) [12] при
определяется рядом IX (48’) [12] при 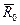 =0.
=0.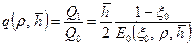 , (11.5.4)
, (11.5.4)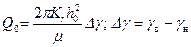 ; (11.5.5)
; (11.5.5)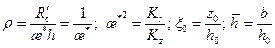 . (11.5.6)
. (11.5.6)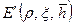 по параметру
по параметру 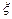 .
.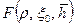 фигурирует формула
фигурирует формула 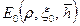 , определяемая по уравнению (11.5.3).
, определяемая по уравнению (11.5.3). ; 8 – отношения радиуса контура питания к начальной толщине пласта; æ;*=0,25; 2,5 – коэффициенты анизотропии;
; 8 – отношения радиуса контура питания к начальной толщине пласта; æ;*=0,25; 2,5 – коэффициенты анизотропии; 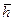 =0,1; 0,8 – относительные вскрытия пласта. Требуется рассчитать предельные безводные дебиты для случаев притока нъютоновской и ненъютоновской нефти.
=0,1; 0,8 – относительные вскрытия пласта. Требуется рассчитать предельные безводные дебиты для случаев притока нъютоновской и ненъютоновской нефти.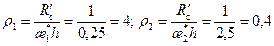 .
.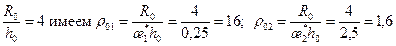 .
.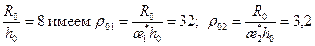 .
.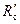 — радиус внутренней зоны, равный
— радиус внутренней зоны, равный 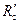 = h (см. рис. 11.2).
= h (см. рис. 11.2).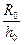 и задаваемых значений x по формуле (11.5.3) находим значения функции
и задаваемых значений x по формуле (11.5.3) находим значения функции 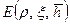 и строим зависимость
и строим зависимость  (рис.11.9).. Значение функции
(рис.11.9).. Значение функции  подсчитываем затем по формуле (11.5.4). Для сравнения рассчитывались значения предельных дебитов в случае притока нъютоновской жидкости и обычных вязких в равных условиях [12]. При этом дебиты
подсчитываем затем по формуле (11.5.4). Для сравнения рассчитывались значения предельных дебитов в случае притока нъютоновской жидкости и обычных вязких в равных условиях [12]. При этом дебиты 
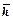 )
)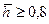 ) разница несущественна (порядка 0-1,5%), тогда как для малых вскрытий эта разница достигает порядка 25%. Кроме того, при æ;*=0,25, т. е. когда проницаемость вдоль вертикали k z больше проницаемости по горизонтали в 16 раз, то при вскрытии
) разница несущественна (порядка 0-1,5%), тогда как для малых вскрытий эта разница достигает порядка 25%. Кроме того, при æ;*=0,25, т. е. когда проницаемость вдоль вертикали k z больше проницаемости по горизонтали в 16 раз, то при вскрытии 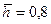 , при любом практически дебите, поверхность раздела не будет устойчивой. Увеличение анизотропии в 10 раз ведет к увеличению безразмерного дебита в два раза как для
, при любом практически дебите, поверхность раздела не будет устойчивой. Увеличение анизотропии в 10 раз ведет к увеличению безразмерного дебита в два раза как для 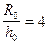 , так и для
, так и для 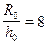 .
. , где значение Q 0 подсчитываетсяпо формуле (11.5.5), включающей в себя
, где значение Q 0 подсчитываетсяпо формуле (11.5.5), включающей в себя 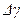 и m. Обычно для вязкопластичных жидкостей
и m. Обычно для вязкопластичных жидкостей 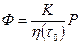 (τ;0 –динамическое напряжение сдвига), т. е. решение для распределения потенциала в пласте будет таким же, как и для обычной нъютоновской жидкости. Безразмерный предельный дебит
(τ;0 –динамическое напряжение сдвига), т. е. решение для распределения потенциала в пласте будет таким же, как и для обычной нъютоновской жидкости. Безразмерный предельный дебит 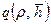 может быть рассчитано по обычной методике для вязких жидкостей, а размерный дебит по формуле (11.5.5) с заменой m на
может быть рассчитано по обычной методике для вязких жидкостей, а размерный дебит по формуле (11.5.5) с заменой m на 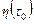 .
.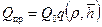 с учетом (11.5.4). Для забойного давления Р с формула примет вид
с учетом (11.5.4). Для забойного давления Р с формула примет вид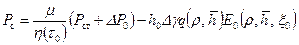 . (11.5.7)
. (11.5.7)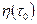 – коэффициент структурной вязкости вязкопластичной нефти в пластовых условиях, как функция динамического напряжения сдвига τ0;
– коэффициент структурной вязкости вязкопластичной нефти в пластовых условиях, как функция динамического напряжения сдвига τ0;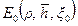 – oпpeдeляeтcя по формуле (11.5.3) при
– oпpeдeляeтcя по формуле (11.5.3) при 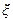 =
=  .
.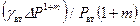 , а для распределения давления необходимо Р заменить на
, а для распределения давления необходимо Р заменить на 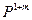 .
.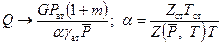 , (11.5.8)
, (11.5.8)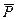 – средневзвешенное пластовое давление в зоне дренирования;
– средневзвешенное пластовое давление в зоне дренирования;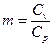 (Cv и Ср – соответственно удельные теплоемкости газа при постоянном объеме и давлении).
(Cv и Ср – соответственно удельные теплоемкости газа при постоянном объеме и давлении).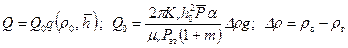 ; (11.5.9)
; (11.5.9)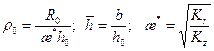 , (11.5.10)
, (11.5.10)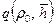 – безразмерный предельный безводный дебит, определяемый по графикам или таблицам (см. § 11.2);
– безразмерный предельный безводный дебит, определяемый по графикам или таблицам (см. § 11.2);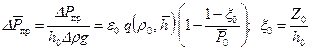 ; (11.5.11)
; (11.5.11) , (11.5.12)
, (11.5.12)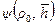 – некоторая функция, определяемая по таблицам или графикам (см. табл. 11.2, рис. 9.2).
– некоторая функция, определяемая по таблицам или графикам (см. табл. 11.2, рис. 9.2).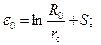 , (11.5.13)
, (11.5.13) , (11.5.15)
, (11.5.15)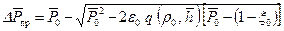 . (11.5.16)
. (11.5.16)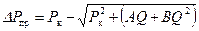 . (11.5.17)
. (11.5.17)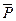 )=0,846; Z (Р ат)=0,9; ρ;в=978 кг/м3; ρ;г=70 кг/м3; μ;г=0,0111 мПа.с; r с=0,1 м; æ;*=6,68; h 0=10 м;
)=0,846; Z (Р ат)=0,9; ρ;в=978 кг/м3; ρ;г=70 кг/м3; μ;г=0,0111 мПа.с; r с=0,1 м; æ;*=6,68; h 0=10 м; 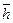 =0,80; R 0=100 м; K =1,068 мкм2; m =12 отв/м – плотность перфорации; 2 r 0=0,0127 м – диаметр префорационного отверстия; l 0=0,345 м – глубина канала.
=0,80; R 0=100 м; K =1,068 мкм2; m =12 отв/м – плотность перфорации; 2 r 0=0,0127 м – диаметр префорационного отверстия; l 0=0,345 м – глубина канала.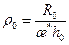
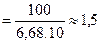 значения безразмерной ординаты вершины конуса
значения безразмерной ординаты вершины конуса 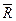 )=8,3;
)=8,3;