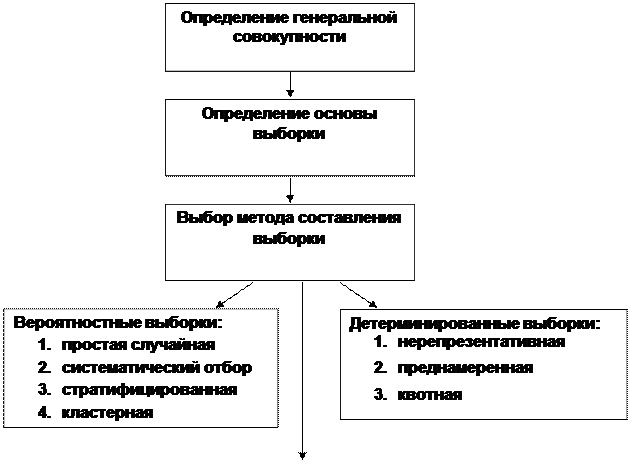
Выборка типических единиц
При использовании данного метода отбираются единицы генеральной совокупности, обладающие средним (или типичным) значением признака. Однако в таком случае встает проблема выбора признака и определения его типичного значения. Субъективный характер оценки вполне может привести к систематической ошибке. Данный метод целесообразно применять для изучения таких объектов, о которых мы уже обладаем некоторой информацией, например, территориальных общностей, предприятий, учреждений и т.п Квотные выборки (quota sampling) – детерминированные выборки, формируемые путём включения в выборку элементов в той же пропорции по основным характеристикам, в которой они присутствуют в общей исследуемой совокупности Квотная выборка - один из наиболее популярных методов формирования выборки. При использовании квотного метода отбирают один или несколько признаков, по которым будет контролироваться выборка. Требования к выборке могут быть жесткими и пониженными. Жесткие требования означают полное совпадение пропорций генеральной и выборочной совокупностей по сочетаниям признаков. В этом случае структура выборочной и генеральной совокупностей по заданным параметрам точно совпадают. При использовании пониженных (частичных) требований контролируют лишь совпадение пропорций по каждому параметру отдельно. Преимущества: контроль за важнейшими параметрами выборки, Квотная выборка точнее собственно случайной при равном объеме. Недостатки: необходимо предварительное изучение объекта для выявления в нем пропорций единиц с различными характеристиками и связей между характеристиками. При формировании выборки необходимо выполнить следующие этапы: Проектирование выборки
Определение объема выборки. В реальности решение об объеме выборки является компромиссом между теоретическими предположениями о точности результатов обследования и возможностями их практической реализации, прежде всего имеются в виду затраты на проведение опроса. Известно, что чем больше объем выборки, тем меньше ее ошибка. Однако необходимо учитывать, что, стоимость выборки растет пропорционально ее объему, а ошибка выборки уменьшается по норме, равной квадратному корню из относительного роста размера выборки. Если размер выборки увеличить в 4 раза, то ошибка выборки уменьшится только на половину. Оптимальный объём выборки зависит от следующих параметров: · типа выборки; · изучаемых характеристик и их распределения в генеральной совокупности; · доступных ресурсов (финансовых, временных) для исследования. На практике используется несколько подходов к определению объема выборки. Произвольный подход основан на применении «правила большого пальца». Например, бездоказательно принимается, что для получения точных результатов выборка должна составлять 5% от генеральной совокупности. Объем выборки может быть установлен исходя из некоторых заранее оговоренных условий. Например, заказчик знает, что при изучении общественного мнения выборка обычно составляет 1000 - 1200 человек, поэтому он рекомендует исследователю придерживаться данной цифры. В случае, если на каком-то рынке проводятся ежегодные исследования, то в каждом году используется выборка одного и того же объема. Объем выборки может определяться на основе статистического анализа. Этот подход основан на определении минимального объема выборки исходя из требований к надежности и достоверности получаемых результатов. При определении объёма выборки исследователь использует два основных статистических параметра: точность оценки и степень достоверности оценки. Точность оценки – величина ошибки результата в абсолютном или относительном выражении. Степень достоверности оценки – вероятность того, что оценка соответствует истинному значению при установленной точности, т.е. вероятность гарантирующая результат. Доверительный интервал – это диапазон, крайним точкам которого соответствует определенный процент определенных ответов на какой-то вопрос. Значение нормированного отклонения оценки (z) от среднего значения в зависимости от доверительной вероятности (
Для выборок достаточно большого объёма (больше 30 элементов) при оценке уровня среднего значения признака в генеральной совокупности, объём определяется по следующей формуле:
где: n – объём выборки; z – нормированное отклонение, соответствующее принятому уровню доверительной вероятности (то есть вероятности, с которой истинное значение признака в генеральной совокупности будет соответствовать значению признака в выборочной совокупности), определяется по статистическим таблицам; e2 – предельная ошибка выборки (то есть величина, устанавливающая границы интервала относительно выборочного среднего значения, в которые с указанной доверительной вероятностью попадёт генеральное среднее значение изучаемого признака); σ² - дисперсия исследуемого признака в генеральной совокупности;
N – объем генеральной совокупности При любом виде проектируемой выборки расчет ее объема производят по формуле повторного отбора. Если доля последнего превысит 5 % от генеральной совокупности, то переходят к расчету по формуле бесповторного отбора. Если доля выборочной совокупности будет меньше 5 %, то к формуле бесповторного отбора не переходят, т.к. это существенно не скажется на величине выборки.
Величина σ² зачастую бывает неизвестна, поэтому используют приближенные способы ее оценки:
Возможно определение объема выборки на основе процентных величин. Например, исследуется мнение потребителей о новом продукте и заказчик данного исследования указал, что его устроит точность полученных результатов, равная Когда на исходный вопрос существует только два варианта ответа, выраженное в % (например, 30% респондентов будет покупать новый продукт, а 70% не будет покупать новый продукт), объем выборки определяется по следующей формуле:
где n – объем выборки; z – нормированное отклонение, определяемое исходя из выбранного уровня доверительности; р – найденная вариация для выборки; q = (100 – p); e – допустимая ошибка. При использовании процентной меры изменчивости принимается в расчет то обстоятельство, что максимальная изменчивость достигается для p = 50%, что является наихудшим случаем. Иногда, когда невозможно определить вариацию для выборки используют максимальную меру изменчивости. Приведенные формулы расчета объема выборки основаны на предположении, что все правила формирования выборки были соблюдены и единственной ошибкой выборки является ошибка, обусловленная ее объемом. Однако, следует помнить, что объем выборки определяет точность полученных результатов, но не их представительность, которая определяется методом формирования выборки. Расчетные формулы, применяемые в маркетинговых исследованиях
|



 ) полученного результата.
) полученного результата. 5%. Предположим, что 30% членов выборки высказалось за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25% – 35%. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.
5%. Предположим, что 30% членов выборки высказалось за новый продукт. Это означает, что диапазон возможных оценок для всей совокупности составляет 25% – 35%. Причем, чем больше объем выборки, тем меньше ошибка. Высокое значение вариации обусловливает высокое значение ошибки и наоборот.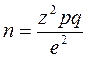 ,
,


