Метод максимального правдоподобия. Функция правдоподобия в непрерывном и дискретном случаях. Оценка максимального правдоподобия и их основные свойства.
Метод наибольшего правдоподобия. Пусть Х – дискретная случайная величина, которая в результате п испытаний приняла значения х 1, х 2, …, хп. Предположим, что нам известен закон распределения этой величины, определяемый параметром Θ, но неизвестно численное значение этого параметра. Найдем его точечную оценку. Пусть р (хi, Θ) – вероятность того, что в результате испытания величина Х примет значение хi. Назовем функцией правдоподобия дискретной случайной величины Х функцию аргумента Θ, определяемую по формуле: L (х 1, х 2, …, хп; Θ) = p (x 1,Θ) p (x 2,Θ)… p (xn,Θ). Тогда в качестве точечной оценки параметра Θ принимают такое его значение Θ* = Θ(х 1, х 2, …, хп), при котором функция правдоподобия достигает максимума. Оценку Θ* называют оценкой наибольшего правдоподобия. Поскольку функции L и ln L достигают максимума при одном и том же значении Θ, удобнее искать максимум ln L – логарифмической функции правдоподобия. Для этого нужно: 1)найти производную 2)приравнять ее нулю (получим так называемое уравнение правдоподобия) и найти критическую точку; 3)найти вторую производную Достоинства метода наибольшего правдоподобия: полученные оценки состоятельны (хотя могут быть смещенными), распределены асимптотически нормально при больших значениях п и имеют наименьшую дисперсию по сравнению с другими асимптотически нормальными оценками; если для оцениваемого параметра Θ существует эффективная оценка Θ*, то уравнение правдоподобия имеет единственное решение Θ*; метод наиболее полно использует данные выборки и поэтому особенно полезен в случае малых выборок. Недостаток метода наибольшего правдоподобия: сложность вычислений. Для непрерывной случайной величины с известным видом плотности распределения f (x) и неизвестным параметром Θ функция правдоподобия имеет вид: L (х 1, х 2, …, хп; Θ) = f (x 1,Θ) f (x 2,Θ)… f (xn,Θ). Оценка наибольшего правдоподобия неизвестного параметра проводится так же, как для дискретной случайной величины.
|

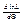 ;
;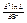 ; если она отрицательна в критической точке, то это – точка максимума.
; если она отрицательна в критической точке, то это – точка максимума.


