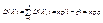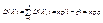Биномиальное распределение.
Для дискретной случайной величины Х, представляющей собой число появлений события А в серии из п независимых испытаний (см. лекцию 6), М (Х) можно найти, используя свойство 4 математического ожидания. Пусть Х 1 – число появлений А в первом испытании, Х 2 – во втором и т.д. При этом каждая из случайных величин Хi задается рядом распределения вида
Следовательно, М (Хi) = p. Тогда 
Аналогичным образом вычислим дисперсию: D (Xi) = 0²· q + 1²· p – p ² = p – p ² = p (1 – p), откуда по свойству 4 дисперсии