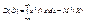Числовые характеристики непрерывных случайных величин.
Распространим определения числовых характеристик случайных величин на непре-рывные случайные величины, для которых плотность распределения служит в некото-ром роде аналогом понятия вероятности. Определение 7.7. Математическим ожиданием непрерывной случайной величины называется
Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной (опр. 7.5), а формула для ее вычисления имеет вид:
Среднее квадратическое отклонение вычисляется по формуле. Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [ a, b ], то интегралы в формулах (7.13) и (7.14) вычисля-ются в этих пределах.
|
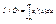Замечание 1.
