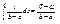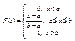Равномерный закон распределения. Часто на практике мы имеем дело со случайными величинами, распределенными определенным типовым образом
Часто на практике мы имеем дело со случайными величинами, распределенными определенным типовым образом, то есть такими, закон распределения которых имеет некоторую стандартную форму. В прошлой лекции были рассмотрены примеры таких законов распределения для дискретных случайных величин (биномиальный и Пуассона). Для непрерывных случайных величин тоже существуют часто встречающиеся виды закона распределения, и в качестве первого из них рассмотрим равномерный закон. Закон распределения непрерывной случайной величины называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение (f (x) = const при a ≤ x ≤ b, f (x) = 0 при x < a, x > b. Найдем значение, которое принимает f (x) при Вероятность попадания равномерно распределенной случайной величины на интервал Вид функции распределения для нормального закона:
|
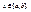Из условия нормировки следует, что 
откуда 
.
равна при этом 
