Показательное распределение.
Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью
В отличие от нормального распределения, показательный закон определяется только одним параметром λ;. В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно. Понятно, что оценить один параметр проще, чем несколько. Найдем функцию распределения показательного закона:
Теперь можно найти вероятность попадания показательно распределенной случайной величины в интервал (а, b):
Значения функции е-х можно найти из таблиц.
|
(6.5)
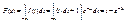Следовательно,
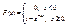(6.6)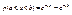
. (6.7)
