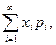Формы представления законов распределения вероятностей и их числовые характеристики. Определение параметров распределения случайной величины.

Закон распределения полностью характеризует случайную величину. Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями. Иногда даже выгоднее пользоваться числами, которые описывают случайную величину суммарно; такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относится математическое ожидание.

Математическое ожидание, как будет показано далее, приближенно равно среднему значению случайной величины.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Пусть случайная величина X может принимать только значения х ₁, х ₂,..., х_п, вероятности которых соответственно равны р _1, р ₂,..., р_п. Тогда математическое ожидание М (X)случайной величины X определяется равенством

М (X) = х ₁ р ₁ + х ₂ р ₂ + … + x_np_n.

Если дискретная случайная величина X принимает счетное множество возможных значений,то М (Х) =

причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

6.Закон распределения вероятностей дискретной случайной величины и его формы: аналитическая, табличная,графическая. Случайная величина непрерывного типа.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:

Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события X = х ₁, X = х ₂,..., X = х_п образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице:

p ₁ +p ₂ + …+p_n= 1.

Если множество возможных значений X бесконечно (счетно), то ряд p ₁ +p ₂ + … сходится и его сумма равна единице.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.