Плотность распределения вероятностей. Функция распределения вероятностей. Их свойства.
Непрерывную случайную величину можно также задать, используя другую функцию, которую называют плотностью распределении или плотностью вероятности (иногда ее называют дифференциальной функцией). Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (х)— первую производную от функции распределения F (х): f (х)= F' (х). Из этого определения следует, что функция распределения является первообразной для плотности распределения. Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима. Функцией распределения называют функцию F (x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т. е. F (x) =P (X < х). Геометрически это равенство можно истолковать так: F (х)есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х. Иногда вместо термина «функция распределения» используют термин «интегральная функция». Теперь можно дать более точное определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Свойство 1. Значения функции распределения принадлежат отрезку [О, 1]: 0 Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы. Свойство 2. F (х)— неубывающая функция, т. е. F (x 2) Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F(x) = 0 при х Доказательство. 1) Пусть x1 2) Пусть х2 Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:
8.Числовые характеристики распределения случайной величины: математическое ожидание, дисперсия, среднее квадратичное отклонение. Их свойства. Понятие о начальных и центральных, моментов, связи между ними. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Пусть случайная величина X может принимать только значения х 1, х 2,..., хп, вероятности которых соответственно равны р 1, р 2,..., рп. Тогда математическое ожидание М (X)случайной величины X определяется равенством М (X) = х 1 р 1 + х 2 р 2 + … + xnpn. Если дискретная случайная величина X принимает счетное множество возможных значений, то М (Х) = причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно. Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: М (С) = С. Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ)=СМ(Х).
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY) = M(X)M(Y). Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: М (X + Y) = М (X) + М (Y). Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D (X) = M [ X — M (X)]2 Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания: D (X) = М (X 2) — [ M (X)]2. Свойство 1. Дисперсия постоянной величины С равна нулю: D (С) = 0. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(CX)=C2D(X). Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X + Y) = D(X) + D(Y). Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X-Y)=D(X)+D(Y). Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии: s (X)= Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность (X)совпадает сразмерностью X. Начальным моментом порядка k случайной величины X называют математическое ожидание величины Xk: vk = M (X). В частности, v 1 = M (X), v 2 = M (X 2). Пользуясь этими моментами, формулу для вычисления дисперсии D (X) = M (X 2)— [ М (X)]2 можно записать так: D (X) = v 2 – Центральным моментом порядка k случайной величины X называют математическое ожидание величины (Х-М(Х))k:
В частности,
Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая (*) и (***), получим v 2 – Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы: v 3 – 3 v 2 v 1 + 2 v 4 – 4 v 3 v 1 + 6 v 2 9. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:
Приняв во внимание, что в одном испытании случайная величина принимает одно и только одно возможное значение, заключаем, что события X = х 1, X = х 2,..., X = хп образуют полную группу; следовательно, сумма вероятностей этих событий, т. е. сумма вероятностей второй строки таблицы, равна единице: p 1 +p 2 + …+pn= 1. Если множество возможных значений X бесконечно (счетно), то ряд p 1 +p 2 + … сходится и его сумма равна единице. Пусть производится п независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна р (следовательно, вероятность непоявления q =1— р). Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях. Поставим перед собой задачу: найти закон распределения величины X. Для ее решения требуется определить возможные значения X и их вероятности. Очевидно, событие А в п испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза,..., либо п раз. Таким образом, возможные значения X таковы: х 1 = 0, x 2 = 1, х 3 = 2 ,..., хп+ 1 = п. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли: Pn (k) = где k = 0, 1, 2,.... п. Формула (*) и является аналитическим выражением искомого закона распределения. Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (*) можно рассматривать как общий член разложения бинома Ньютона: (p + q) n = Таким образом, первый член разложения рп определяет вероятность наступления рассматриваемого события п раз в п независимых испытаниях; второй член npn- 1 q определяет вероятность наступления события п —1 раз;...; последний член qn определяет вероятность того, что событие не появится ни разу. Напишем биномиальный закон в виде таблицы:
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же п велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (р Итак, поставим перед собой задачу найти вероятность того,что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение пр сохраняет постоянное значение, а именно пр = Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности: Pn (k) = Так как рп = Pn (k) = Приняв во внимание, что п имеет очень большое значение, вместо Рn (к)найдем Итак,
Таким образом (для простоты записи знак приближенного равенства опущен), Pn (k) = Эта формула выражает закон распределения Пуассона вероятностей массовых (п велико) и редких (р мало) событий.
Потоком событий называют последовательность событий, которые наступают в случайные моменты времени. Среди свойств, которыми могут обладать потоки, выделим свойства стационарности, отсутствия последействия и ординарности. Свойство стационарности характеризуется тем, что вероятность появления k событий на любом промежутке от времени зависит только от числа k и от длительности t промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися. если поток обладает свойством, стационарности, то вероятность появления k событий за промежуток времени длительности t есть функция, зависящая только от k и t. Свойство отсутствия последействия характеризуется тем, что вероятность появления k событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. если поток обладает свойством отсутствия последействия, то имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени. Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно. Другими словами, вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью появления только одного события. Итак, если поток обладает свойством ординарности, то за бесконечно малый промежуток времени может появиться не более одного события. Простейшим (пуассоновским)называют поток событий, который обладает свойствами стационарности, отсутствия последействия и ординарности. если поток представляет собой сумму очень большого числа независимых стационарных потоков, влияние каждого из которых на всю сумму (суммарный поток) ничтожно мало, то суммарный исток (при условии его ординарности) близок к простейшему. Интенсивностью потока Можно доказать, что если постоянная интенсивность потока известна, то вероятность появления k событий простейшего потока за время длительностью t определяется формулой Пуассона
Pt (k) = Эта формула отражает все свойства простейшего потока. Действительно, из формулы видно, что вероятность появления k событий за время t, при заданной интенсивности является функцией k и t, что характеризует свойство стационарности. Формула не использует информации о появлении событий до начала рассматриваемого промежутка, что характеризует свойство отсутствия последействия. Убедимся, что формула отражает свойство ординарности. Положив k = 0и k= 1, найдем соответственно вероятности непоявления событий и появления одного события: Pt (0) = Следовательно, вероятность появления более одного события Pt (k>;1) = 1 - [ Pt (0) +Pt (1)] = 1 - [ Пользуясь разложением
после элементарных преобразований получим Pt (k> 1) = ( Сравнивая Рt (1) и Pt (k>;1), заключаем, что при малых значениях t вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью наступления одного события, что характеризует свойство ординарности.
|

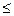 F (х)
F (х) 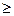 F (х 1), если х 2> х 1.
F (х 1), если х 2> х 1.
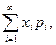

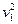 . (*)
. (*)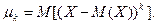
 (**)
(**)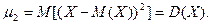 (***)
(***)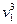 ,
, .
. (*)
(*)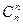 pn +
pn +  pn- 1 q +… +
pn- 1 q +… +  pkqn-k+…+
pkqn-k+…+  qn
qn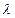 . Как будет следовать из дальнейшего (см. гл. VII, § 5), это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях п, остается неизменным.
. Как будет следовать из дальнейшего (см. гл. VII, § 5), это означает, что среднее число появлений события в различных сериях испытаний, т. е. при различных значениях п, остается неизменным.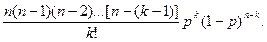
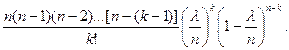
 Pn (k). При этом будет найдено лишь приближенное значение отыскиваемой вероятности: п хотя и велико, но конечно, а при отыскании предела мы устремим п к бесконечности. Заметим, что поскольку произведение пр сохраняет постоянное значение, то при п
Pn (k). При этом будет найдено лишь приближенное значение отыскиваемой вероятности: п хотя и велико, но конечно, а при отыскании предела мы устремим п к бесконечности. Заметим, что поскольку произведение пр сохраняет постоянное значение, то при п 
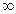 вероятность р
вероятность р 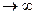 .
.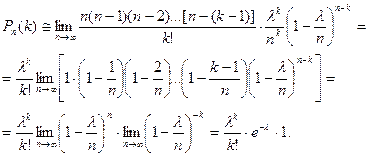

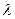 называют среднее число событий, которые появляются в единицу времени.
называют среднее число событий, которые появляются в единицу времени.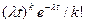 .
. , Pt (1) =
, Pt (1) = 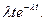
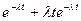 ].
].



