Модель факторного анализа
Факторный анализ Как и прежде будем полагать, что Х = (X 1, X 2, …, Xk)T — исходный k -мерный случайный вектор. Каноническая модель факторного анализа для центрированного вектора
где F = (F 1, F 2, …, Fm) — центрированный и нормированный случайный вектор некоррелированных m общих факторов для всех исходных случайных величин Xi (m < k), Пусть Построим систему уравнений для нахождения матриц A и Σε. С учетом (16) и условий на векторах F и
Итак,
или
Таким образом, здесь, в отличие от модели главных компонент, ковариации исходных случайных величин полностью воспроизводятся матрицей нагрузок, а для воспроизведения их дисперсий помимо нагрузок нужны дисперсии u i специфических факторов. И далее, так как
то здесь, как и в компонентном анализе, ковариации Замечание. Если исходный k -мерный вектор Х не только центрирован, но и нормирован, то ΣХ — это корреляционная матрица RХ и система (17) примет вид RХ = AA T+ Σε или
и в этом случае Величину В системе (17) k 2 уравнений, а число неизвестных (aij и υ i) равно mk + k < < k (k + 1). Если допустить, что k, m и матрица ΣХ таковы, что решение этой системы существует (иначе построение модели (16) допустимо?), то это решение не единственно. Действительно, пусть V — ортогональная матрица размером
В преобразованной модели вектор общих факторов — это вектор Итак, если решение системы (17) существует, то оно не единственно: допустим целый класс матриц нагрузок, которые связаны между собой ортогональными преобразованиями. Замечание. В методе главных компонент также допустимо ортогональное преобразование матрицы нагрузок. Однако вращение пространства главных компонент меняет вклады компонент в общую дисперсию исходных случайных величин: они не равны собственным значениям. При каких дополнительных условиях на k, m и матрицу нагрузок А решение системы (17) единственно с точностью до ортогонального преобразования? Матрица А должна быть такой, чтобы при вычеркивании из нее любой строки оставшуюся матрицу можно было бы разделить на две подматрицы ранга m (откуда получаем, что 2 m „ k — 1). Сформулированное требование к матрице А является не только достаточным, но и при m = 1и m = 2необходимым условием единственности решения системы (17). Будем предполагать, что решение единственно с точностью до ортогонального преобразования. Тогда, вращая систему координат в m -мерном пространстве общих факторов, можно найти такую матрицу нагрузок, которая позволила бы дать содержательную интерпретацию общих факторов в терминах исходных случайных величин. Существует несколько вариантов дополнительных условий на класс матриц А, обеспечивающих уже окончательную однозначность решения. От этих условий зависит и метод нахождения матриц А, Σε, вектора F, и, соответственно, способ их статистического оценивания. Наиболее формализованы следующие варианты дополнительных идентифицирующих требований к виду матрицы А: 1) матрица 2) матрица A T B (где матрица
т. е. исходный признак Х 1 выражается только через общий фактор F 1; X 2 — через F 1 и F 2 и т. д. Общая итерационная схема нахождения (при заданном m) параметров (А, Σε) факторной модели такова: · задаются нулевым приближением · получают нулевое приближение · последовательно определяют нулевые приближения Замечание. Нетрудно убедиться в том, что · определяют первые приближения · итерационный процесс заканчивают, когда очередное приближение матрицы Σε мало отличается от предыдущего. В реальных задачах располагают лишь оценкой
|

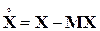 имеет следующий вид:
имеет следующий вид: (2.3.1)
(2.3.1) — (неслучайная) матрица нагрузок случайных величин Xi на факторы Fj,
— (неслучайная) матрица нагрузок случайных величин Xi на факторы Fj,  — нормально распределенный центрированный вектор e специфических факторов e1, e2, …, e k, некоррелированных как между собой, так и с общими факторами.
— нормально распределенный центрированный вектор e специфических факторов e1, e2, …, e k, некоррелированных как между собой, так и с общими факторами.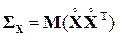 — ковариационная матрица вектора Х, а Σε =
— ковариационная матрица вектора Х, а Σε = 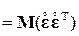 — ковариационная матрица (диагональная) вектора e с диагональными элементами, равными
— ковариационная матрица (диагональная) вектора e с диагональными элементами, равными  .
.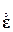 получим:
получим: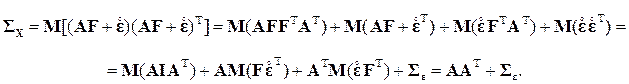

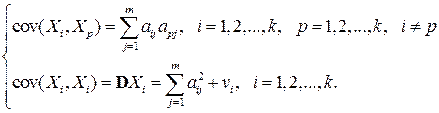 (2.3.2)
(2.3.2) ,
, .
.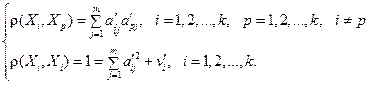 (2.3.3)
(2.3.3)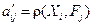 , а
, а  .
. называют общностью случайной величины Хi, а матрицу R ' = A ' A ' T, где
называют общностью случайной величины Хi, а матрицу R ' = A ' A ' T, где  — редуцированной матрицей (R ' отличается от R только тем, что ее диагональными элементами являются не единицы, а общности hi).
— редуцированной матрицей (R ' отличается от R только тем, что ее диагональными элементами являются не единицы, а общности hi).
 . Проведем тождественные преобразования модели (16):
. Проведем тождественные преобразования модели (16): . (2.3.4)
. (2.3.4) , а матрица нагрузок
, а матрица нагрузок  .
.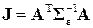 должна иметь диагональный вид с различными расположенными в порядке убывания диагональными элементами;
должна иметь диагональный вид с различными расположенными в порядке убывания диагональными элементами; задана заранее) имеет ранг m и должна быть треугольной (наддиагональной); в частности, при
задана заранее) имеет ранг m и должна быть треугольной (наддиагональной); в частности, при матрица
матрица  ,
, диагональной матрицы Σε (нулевым приближением
диагональной матрицы Σε (нулевым приближением  дисперсий vi специфических факторов);
дисперсий vi специфических факторов); матрицы ψ; = AA T;
матрицы ψ; = AA T; столбцов a 1, a 2, …, am матрицы А;
столбцов a 1, a 2, …, am матрицы А; . Исходя из этого равенства и учитывая специфику выбранного варианта идентифицирующих требований к матрице А, сначала находят столбец а 1. Затем переходят к матрице
. Исходя из этого равенства и учитывая специфику выбранного варианта идентифицирующих требований к матрице А, сначала находят столбец а 1. Затем переходят к матрице  и определяют столбец а 2 и т. д.
и определяют столбец а 2 и т. д.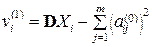 дисперсий vi (первое приближение
дисперсий vi (первое приближение  матрицы Σε) и переходят к следующей итерации;
матрицы Σε) и переходят к следующей итерации; ковариационной матрицы ΣX. Заменив в рассмотренной общей схеме ΣX на
ковариационной матрицы ΣX. Заменив в рассмотренной общей схеме ΣX на 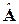 и
и  соответственно матрицы нагрузок А и ковариационной матрицы Σε специфических факторов.
соответственно матрицы нагрузок А и ковариационной матрицы Σε специфических факторов.


