Реализация описанной общей итерационной схемы для первого варианта идентифицирующего требования к виду матрицы А приводит к оценкам максимального правдоподобия параметров aij  и vi — оценкам, получаемым методом максимального правдоподобия для модели (16) при постулировании нормальности распределения наблюдений вектора Х с учетом указанного требования. При достаточно общих ограничениях оценки максимального правдоподобия
и vi — оценкам, получаемым методом максимального правдоподобия для модели (16) при постулировании нормальности распределения наблюдений вектора Х с учетом указанного требования. При достаточно общих ограничениях оценки максимального правдоподобия 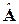 и
и  асимптотически нормальны, несмещены и эффективны.
асимптотически нормальны, несмещены и эффективны.
Можно доказать, что при максимизации логарифмической функции правдоподобия с учетом требования 1) диагональными элементами матрицы  будут первые m наибольших собственных значений матрицы
будут первые m наибольших собственных значений матрицы 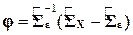 , а соответствующие собственные векторы будут столбцами матрицы
, а соответствующие собственные векторы будут столбцами матрицы 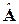 . Поэтому итерационная схема нахождения оценок
. Поэтому итерационная схема нахождения оценок 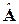 и
и  при заданном m примет следующий вид:
при заданном m примет следующий вид:
· задаются нулевыми приближениями  дисперсий
дисперсий 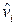 специфических факторов, или иначе задаются нулевым приближением
специфических факторов, или иначе задаются нулевым приближением 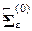 матрицы
матрицы  ;
;
· получают нулевое приближение 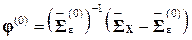 матрицы φ;;
матрицы φ;;
· находят  — наибольшее собственное значение матрицы φ;(0) и соответствующий ему собственный вектор
— наибольшее собственное значение матрицы φ;(0) и соответствующий ему собственный вектор  — это столбец
— это столбец 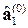 матрицы
матрицы  ; в φ;(0) матрицу
; в φ;(0) матрицу  заменяют на
заменяют на  и для новой матрицы φ;(0) находят наибольшее собственное значение
и для новой матрицы φ;(0) находят наибольшее собственное значение  и соответствующий ему собственный вектор — это будет столбец
и соответствующий ему собственный вектор — это будет столбец  матрицы
матрицы  , и далее до получения m столбцов матрицы
, и далее до получения m столбцов матрицы  ;
;
· получают первое приближение  дисперсии
дисперсии 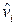 , иначе? первое приближение
, иначе? первое приближение 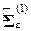 матрицы
матрицы  и переходят к следующей итерации.
и переходят к следующей итерации.
1.1.2 Факторный анализ показателей…
Используя процедуру метода максимального правдоподобия, проведем факторный анализ шести экономических показателей (см. стр.), при этом примем m = 2,  , где
, где  и
и  — нагрузки показателя Хi на первые две компоненты. Результаты одной итерации приведены в табл. 2.3.1.
— нагрузки показателя Хi на первые две компоненты. Результаты одной итерации приведены в табл. 2.3.1.
Таблица 2.3.1

| 0,4112
| 0,3728
| 0,3903
| 0,5296
| 0,5875
| 0,4328
|
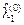
| 4,1433
|

| 0,6952
| 0,6267
| 0,3835
| 0,1928
| 0,4604
| 0,5379
|

| 2,4759
|

| 0,0170
| –0,4266
| 0,5779
| 0,5065
| 0,1759
| –0,3220
|

| 0,5164
| 0,4252
| 0,5189
| 0,7063
| 0,7571
| 0,6070
|
Окончательные оценки нагрузок и дисперсий специфических факторов указаны в табл. 2.3.2:
Таблица 2.3.2
| Показатель
| Оценки нагрузок на факторы
| 
| 
|
| F1
| F2
|
| | X1
| 0,6627
| –0,0519
| 0,4419
| 0,5581
| |
| | X2
| 0,5895
| –0,3634
| 0,4796
| 0,5204
| |
| | X3
| 0,3967
| 0,5950
| 0,5114
| 0,4886
| |
| | X4
| 0,1749
| 0,2642
| 0,1004
| 0,8996
| |
| | X5
| 0,4463
| 0,1808
| 0,2319
| 0,7681
| |
| | X6
| 0,4618
| –0,2575
| 0,2796
| 0,7204
| |
| | Оценка доли вклада Fj
в общую дисперсию, %

| 23,12
| 10,96
|
|
| |
| | | | | | | | | |
Допустимо ли представление исходного вектора Х с помощью модели (16) факторного анализа с числом общих факторов, равным m (в примере m = 2). Гипотеза о том, что число общих факторов равно m отвергается (с вероятностью ошибки, равной a), если
 , (2.3.5)
, (2.3.5)
где число степеней свободы q =.
В примере вместо ковариационной матрицы  использовалась корреляционная матрица
использовалась корреляционная матрица  . Учитывая это, в неравенстве (19): n = 153,
. Учитывая это, в неравенстве (19): n = 153,  ,
,  ,
,  , c2 = 4,95, k = 6, m = 2,
, c2 = 4,95, k = 6, m = 2, 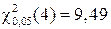 .
.
Так как 4,95 < 9,49, то гипотезу о наличии двух общих факторов не отвергаем при a = 0,05.

 и vi — оценкам, получаемым методом максимального правдоподобия для модели (16) при постулировании нормальности распределения наблюдений вектора Х с учетом указанного требования. При достаточно общих ограничениях оценки максимального правдоподобия
и vi — оценкам, получаемым методом максимального правдоподобия для модели (16) при постулировании нормальности распределения наблюдений вектора Х с учетом указанного требования. При достаточно общих ограничениях оценки максимального правдоподобия 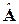 и
и  асимптотически нормальны, несмещены и эффективны.
асимптотически нормальны, несмещены и эффективны. будут первые m наибольших собственных значений матрицы
будут первые m наибольших собственных значений матрицы 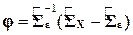 , а соответствующие собственные векторы будут столбцами матрицы
, а соответствующие собственные векторы будут столбцами матрицы  дисперсий
дисперсий 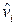 специфических факторов, или иначе задаются нулевым приближением
специфических факторов, или иначе задаются нулевым приближением 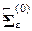 матрицы
матрицы 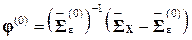 матрицы φ;;
матрицы φ;; — наибольшее собственное значение матрицы φ;(0) и соответствующий ему собственный вектор
— наибольшее собственное значение матрицы φ;(0) и соответствующий ему собственный вектор  — это столбец
— это столбец 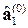 матрицы
матрицы  ; в φ;(0) матрицу
; в φ;(0) матрицу  заменяют на
заменяют на  и для новой матрицы φ;(0) находят наибольшее собственное значение
и для новой матрицы φ;(0) находят наибольшее собственное значение  и соответствующий ему собственный вектор — это будет столбец
и соответствующий ему собственный вектор — это будет столбец  матрицы
матрицы  дисперсии
дисперсии 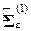 матрицы
матрицы  , где
, где  и
и  — нагрузки показателя Хi на первые две компоненты. Результаты одной итерации приведены в табл. 2.3.1.
— нагрузки показателя Хi на первые две компоненты. Результаты одной итерации приведены в табл. 2.3.1.
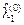







 , (2.3.5)
, (2.3.5) . Учитывая это, в неравенстве (19): n = 153,
. Учитывая это, в неравенстве (19): n = 153,  ,
,  ,
,  , c2 = 4,95, k = 6, m = 2,
, c2 = 4,95, k = 6, m = 2, 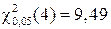 .
.


