Условное представление модели главных компонент.
Для поиска второго фактора ищется ось, перпендикулярная первому фактору, также объясняющая наибольшую часть дисперсии, не объясненной первой осью. После нормировки эта ось становится вторым фактором. Если данные представляют собой плоский элипсоид ("блин") в трехмерном пространстве, два первых фактора позволяют в точности описать эти данные. Таким образом, факторы последовательно выделяются один за другим. Так как каждый последующий фактор определяется так, чтобы максимизировать изменчивость, оставшуюся от предыдущих, то факторы оказываются независимыми друг от друга. Другими словами, некоррелированными или ортогональными. Сколько факторов следует выделять? Максимально возможное число главных компонент равно количеству переменных. Иными словами, если мы хотим на 100% описать значения n переменных, то для этого потребуется столько же, то есть n главных компонент. Сколько главных компонент необходимо построить для оптимального представления рассматриваемых исходных переменных? Имеются некоторые рекомендации, позволяющие рационально выбрать число факторов. Обозначим lk объясненную главной компонентой Fk часть суммарной дисперсии совокупности исходных факторов. По умолчанию, в пакете предусмотрено продолжать строить факторы, пока lк>1. Напомним, что переменные стандартизованы, и поэтому нет смысла строить очередной фактор, если он объясняет часть дисперсии, меньшую, чем приходящуюся непосредственно на одну переменную. При этом следует учесть, что l1>l2>l3,…. К сведению читателя заметим, что значения lk являются собственными значениями корреляционной матрицы Xi, поэтому в выдаче они будут помечены текстом "EIGEN VALUE" (собственные значения). Целесообразно отбирать столько факторов, сколько существует собственных чисел корреляционной матрицы, больших единицы. Данный критерий называется критерием Кайзера. Второй подход базируется на том, что мы сами будем отбирать число факторов, ориентируясь на то, что бы это число факторов объясняло требуемый процент общей исходной дисперсии. Например, если исследователь решает, что факторная модель должна объяснять не менее 75% общей дисперсии исходных переменных. На какой процент объясненной дисперсии необходимо ориентироваться? Не существует каких-то убедительных рекомендаций по определению этого процента, кроме одной, вполне очевидной: «Чем больше, тем лучше». В социологии, как правило, встречаются факторные модели, в которых объясняется 60-75% дисперсии, хотя можно примеры и с большими, и с меньшими процентами. Существует еще один подход, который базируется на методе, так называемой, «каменной осыпи». Суть метода в следующем. Строится график, в котором по оси абсцисс откладываются номера факторов, а по оси ординат – значения собственных чисел, для каждого из факторов. Пример такого рода графика для модели таблицы 5.1 показан на рисунке 5.5. Как говорилось в начале, все собственные числа в методе главных компонент вычисляются в порядке убывания, поэтому график будет представлять собой понижающуюся кривую. Далее на этом графике ищутся точки, в которых происходит более, или менее резкое понижение. Но этот метод часто носит субъективный характер.
Важно понимать, что ни один из изложенных подходов к определению числа факторов не дает нам доказательных оснований по отбору числа факторов.
|

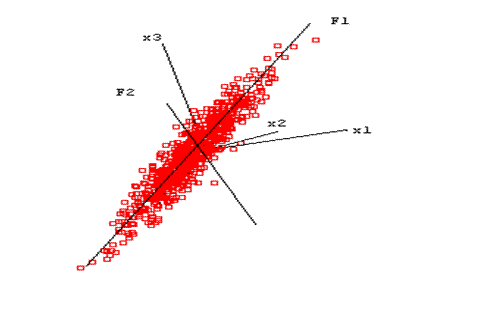 Рисунок 5.2
Рисунок 5.2