Помилки першого та другого роду.
Висунута гіпотеза може бути правильною чи неправильною, тому виникає необхідність її перевірки. Оскільки перевірку проводять статистичними методами, то її називають статистичною. В результаті перевірки гіпотези в двох випадках може бути прийняте неправильне рішення, тобто можуть бути допущені помилки двох родів. Помилка першого роду полягає в тому, що буде відхилена правильна гіпотеза. Помилка другого роду полягає в тому, що буде прийнята неправильна гіпотеза. Наслідки цих помилок різноманітні і можуть мати тяжкі наслідки. _________________________________
61. Елементи дисперсійного аналізу. Однофакторний дисперсійний аналіз. Дисперсійний аналіз. Його сутність полягає в тому, що загальну дисперсію досліджуваної ознаки розділяють на окремі компоненти, які обумовлені впливом певних конкретних чинників. Відповідно до дисперсійного аналізу будь-який його результат можна подати у вигляді суми певної кількості компонент. У разі проведення дисперсійного аналізу досліджуваний масив даних, одержаних під час експерименту, поділяють на певні групи, які різняться дією на результати експерименту певних рівнів факторів. Вважається, що досліджувана ознака має нормальний закон розподілу, а дисперсії в кожній окремій групі здобутих значень ознаки однакові. Ці припущення необхідно перевірити. Однофакторний аналіз. Нехай потрібно дослідити вплив на ознаку Х певного одного фактора. Результати експерименту ділять на певне число груп, які відрізняються між собою ступенем дії фактора. _________________________________
62. Двофакторний дисперсійний аналіз. Нехай необхідно визначити вплив двох факторів А і В на певну ознаку Х. Для цього необхідно, щоб дослід здійснювався при фіксованих рівнях факторів А і В, а також їх одночасній дії на ознаку. При цьому дослід здійснюватимемо n раз для кожного з рівнів факторів А і В. Позначимо через Результат експерименту зручно подати у вигляді таблиці, яка поділена на блоки, в кожному з яких ураховується на певних рівнях факторів А і В їх вплив на конкретні значення ознаки Перелік варіант У=уі, Х=хі та відповідних їм частот утворюють двовимірний статистичний розподіл вибірки, що реалізована з ген. сукупності, елементам цієї вибірки притаманні кількісні ознаки Х і У. Загальні числові характеристики ознаки Х:
Для величини У відповідно. Кореляційний момент, вибірковий коефіцієнт кореляції
Якщо К = 0, то кореляційного зв’язку немає, якщо К≠0, то цей зв'язок існує.
|rB|≤1, -1≤rB ≤1 _________________________________
63. Елементи теорії регресії і кореляції. Показником, що вимірює стохастичний зв’язок між змінними, є коефіцієнт кореляції, який свідчить з певною мірою ймовірності, наскільки зв’язок між змінними близький до строгої лінійної залежності. За наявності кореляційного зв’язку між змінними необхідно виявити його форму функціональної залежності (лінійна чи нелінійна), а саме:
Наведені можливі залежності між змінними X і Y називають функціями регресії. Форму зв’язку між змінними X і Y можна встановити, застосовуючи кореляційні поля, які зображені на рисунках Між ознаками Х та Y може існувати статистична залежність і за відсутності кореляційної. Але коли існує кореляційна залежність між ознаками Х та Y, то обов’язково між ними існуватиме і статистична залежність _________________________________
64. Рівняння лінійної парної регресії. Коефіцієнт кореляції. Рівняння лінійної парної регресії:
де
_________________________________
65. Визначення параметрів в0, в1. У результаті статистичних спостережень дослідник дістає характеристики для незалежної змінної х і відповідні значення залежної змінної у. Отже, необхідно визначити параметри
відповідатиме статистична оцінка
Якщо ми прийняли гіпотезу про лінійну форму зв’язку між ознаками Х і Y, то однозначно вибрати параметри На практиці найчастіше параметри Відповідно до цього методу рівняння лінійної парної регресії
де rxy —парний коефіцієнт кореляції між ознаками X і Y. Тоді
_________________________________ 66. Властивості в0, в1. Точкові статистичні оцінки
Властивості: 1)
2)
3) Статистичні оцінки
_________________________________
67. Довірчі інтервали для в0, в1. Довірчий інтервал для параметра
Довірчий інтервал для параметра
68. Множинна лінійна регресія На практиці здебільшого залежна змінна У цьому разі регресію називають множинною. При цьому якщо аргументи в функції регресії в першій степені, то множинна регресія називається лінійною, у противному разі — множинною нелінійною регресією. Довірчий інтервал для множинної лінійної регресії Матриця Х містить m лінійно незалежних векторів-стовпців, а це означає, що ранг її дорівнюватиме m і визначник Дисперсії статистичних оцінок Коефіцієнт множинної регресіїТісноту між ознаками Y та X, де
Чим ближче значення R до ±1, тим краще вибрано функцію регресії Нормування коефіцієнтів регресії Множинна лінійна регресія дає змогу порівняти вплив на досліджуваний процес різних чинників. У загальному випадку змінні
де
|

 конкретне значення ознаки Х, якого вона набуває при i -му експерименті, j -му рівні фактора A і k -му рівні фактора В.
конкретне значення ознаки Х, якого вона набуває при i -му експерименті, j -му рівні фактора A і k -му рівні фактора В.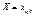
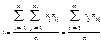
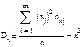

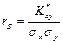
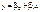 ;
;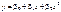 ;
;
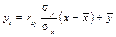
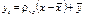 ,
, і називають коефіцієнтом регресії. Для обчислення
і називають коефіцієнтом регресії. Для обчислення 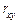 необхідно знайти
необхідно знайти 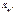
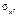
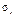
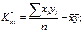
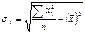 ;
;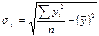 ;
;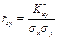
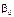 ,
, 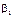 . Але істинні значення цих параметрів дістати неможливо, оскільки ми користуємося інформацією, здобутою від вибірки обмеженого обсягу. Тому знайдені значення параметрів будуть лише статистичними оцінками істинних (невідомих нам) параметрів
. Але істинні значення цих параметрів дістати неможливо, оскільки ми користуємося інформацією, здобутою від вибірки обмеженого обсягу. Тому знайдені значення параметрів будуть лише статистичними оцінками істинних (невідомих нам) параметрів 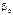 ,
,  , які дістали способом обробки вибірки, моделі
, які дістали способом обробки вибірки, моделі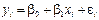
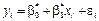 .
. ,
,  , які є точковими статистичними оцінками відповідно для параметрів
, які є точковими статистичними оцінками відповідно для параметрів 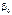 ,
,  .
.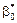 ,
, 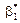 визначаються за методом найменших квадратів, розробка якого належить К. Гауссу і П. Лапласу. Цей метод почали широко застосовувати в економіко-статистичних обчисленнях, відколи була створена теорія регресії.
визначаються за методом найменших квадратів, розробка якого належить К. Гауссу і П. Лапласу. Цей метод почали широко застосовувати в економіко-статистичних обчисленнях, відколи була створена теорія регресії.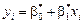 необхідно вибрати так, щоб сума квадратів відхилень спостережуваних значень від лінії регресії була б мінімальною.
необхідно вибрати так, щоб сума квадратів відхилень спостережуваних значень від лінії регресії була б мінімальною. ,
,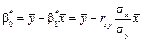 .
.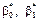 можна подати в такому вигляді:
можна подати в такому вигляді: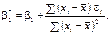 ;
; .
.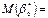
 отже,
отже,  є точковою незміщеною статистичною оцінкою для параметра
є точковою незміщеною статистичною оцінкою для параметра 
 ,
,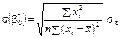 .
.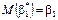 Отже, визначили, що
Отже, визначили, що 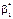 є точковою незміщеною систематичною оцінкою для параметра
є точковою незміщеною систематичною оцінкою для параметра 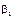
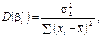

 як випадкові величини впливають на зміщення лінії регресії; так,
як випадкові величини впливають на зміщення лінії регресії; так,  викликає вертикальне зміщення лінії регресії, а
викликає вертикальне зміщення лінії регресії, а  — зміну кута нахилу її.
— зміну кута нахилу її.
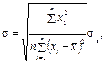
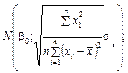
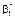 також буде мати нормальний закон розподілу з числовими характеристиками
також буде мати нормальний закон розподілу з числовими характеристиками
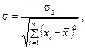
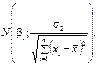

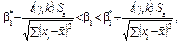 де
де  знаходимо за таблицею за заданою надійністю γ і числом ступенів свободи
знаходимо за таблицею за заданою надійністю γ і числом ступенів свободи 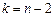 .
.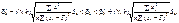 _________________________________
_________________________________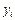 пов’язана з впливом не одного, а кількох аргументів.
пов’язана з впливом не одного, а кількох аргументів.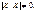 Отже, матриця
Отже, матриця  має обернену.
має обернену.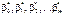 визначають з допомогою кореляційної матриці для вектора
визначають з допомогою кореляційної матриці для вектора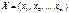 , вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою
, вимірюють з допомогою коефіцієнта множинної кореляції R, що є узагальненням парного коефіцієнта кореляції rij і обчислюється за формулою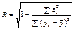 .
.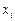 репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою
репрезентують чинники, що мають різні одиниці виміру (кілограми, гривні, метри тощо). Отже, для того щоб порівняти і з’ясувати відносну вагомість кожного з чинників, використовують так звані нормовані коефіцієнти регресії, які визначають за формулою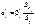
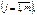
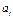 — коефіцієнт регресії після нормування;
— коефіцієнт регресії після нормування; 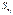 — виправлене середнє квадратичне відхилення змінної
— виправлене середнє квадратичне відхилення змінної 
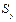 — виправлене середнє квадратичне відхилення ознаки Y.
— виправлене середнє квадратичне відхилення ознаки Y.


